题目内容
某旅游公司为甲，乙两个旅游团提供三条不同的旅游线路，每个旅游团可任选其中一条旅游线路．
（1）求甲，乙两个旅游团所选旅游线路相同的概率．
（2）某天上午9时至10时，甲，乙两个旅游团都到同一个著名景点游览，20分钟后游览结束即离去．求两个旅游团在该著名景点相遇的概率．
（1）求甲，乙两个旅游团所选旅游线路相同的概率．
（2）某天上午9时至10时，甲，乙两个旅游团都到同一个著名景点游览，20分钟后游览结束即离去．求两个旅游团在该著名景点相遇的概率．
考点：几何概型
专题：概率与统计
分析：（1）列举法写出所有基本事件，从中找出符合条件的基本事件，利用基本事件个数比求概率；
（2）用平面区域分布表示实验及满足条件的实验，利用面积比求概率．
（2）用平面区域分布表示实验及满足条件的实验，利用面积比求概率．
解答：
解：（1）用1，2，3表示三条不同的旅游线路，事件用（甲，乙）表示．
基本事件：有（1，1），（1，2），（1，3），（2，1），（2，2），（2，3），（3，1），（3，2），（3，3）共9个．
记“甲，乙两个旅游团所选旅游线路相同”为事件有（1，1），（2，2），（3，3）3个，
∴P(A)=
=
；
（2）设甲，乙两个旅游团到达著名景点的时刻分别为x，y，
则0≤x≤60，0≤y≤60，事件对应区域如图：
两个旅游团在该著名景点相遇，则满足|x-y|≤20，事件对应的区域为图中阴影部分，
∴两个旅游团在著名景点相遇的概率P=
=
=
=
．
基本事件：有（1，1），（1，2），（1，3），（2，1），（2，2），（2，3），（3，1），（3，2），（3，3）共9个．
记“甲，乙两个旅游团所选旅游线路相同”为事件有（1，1），（2，2），（3，3）3个，
∴P(A)=
| 3 |
| 9 |
| 1 |
| 3 |
（2）设甲，乙两个旅游团到达著名景点的时刻分别为x，y，
则0≤x≤60，0≤y≤60，事件对应区域如图：
两个旅游团在该著名景点相遇，则满足|x-y|≤20，事件对应的区域为图中阴影部分，
∴两个旅游团在著名景点相遇的概率P=
| S阴影 |
| S正方形 |
| 60×60-40×40 |
| 60×60 |
| 20 |
| 36 |
| 5 |
| 9 |
点评：本题考查了古典概型的概率计算，考查了几何概型的概率计算，熟练掌握两种概型的特征及管理计算方法是解题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
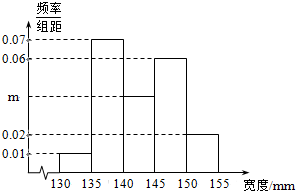1895年，在伦敦有100块男性头盖骨被挖掘出土，经考证，头盖骨的主人死于1665-1666年之间的大瘟疫．人类学家分别测量了这些头盖骨的宽度，得到的频率分布直方图如图所示．
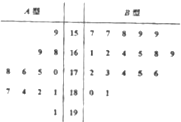某工厂随机抽取处12件A型产品和18件B型产品，将这30件产品的尺寸编成如图所示的茎叶图（单位：cm），若尺寸在175cm以上（包括175cm）的产品定义为“标准件”，尺寸在175cm以下（不包括175cm）的产品定义为“非标准件”