题目内容
已知实数a,b是常数,f(x)=(x+a)2-7blnx+1.
(Ⅰ)若b=1时,f(x)在区间(1,+∞)上单调递增,求a的取值范围.;
(Ⅱ)当b=
a2时,讨论f(x)的单调性;
(Ⅲ)设n是正整数,证明:ln(n+1)7<(1+
+…+
)+7(1+
+…+
).
(Ⅰ)若b=1时,f(x)在区间(1,+∞)上单调递增,求a的取值范围.;
(Ⅱ)当b=
| 4 |
| 7 |
(Ⅲ)设n是正整数,证明:ln(n+1)7<(1+
| 1 |
| 22 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| n |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)由b=1,故f(x)=(x+a)2-7lnx+1,得f′(x)=2x+2a-
.从而a≥
-x在x>1时恒成立.由当x>1时,y=
-x是减函数,从而当x>1时,
-x<
,进而求出a的范围;
(II)由b=
a2,故f(x)=(x+a)2-4a2lnx+1,x∈(0,+∞),求出f′(x)=
=
,
当a=0时,f(x)的增区间为(0,+∞)当a>0时,f(x)的减区间为(0,a)增区间为(a,+∞)当a<0时,f(x)的减区间为(0,-2a)增区间为(-2a,+∞);
(Ⅲ) 由(Ⅰ)知,当a=
时,f(x)=(x+
)2-7lnx+1在(1,+∞)是增函数.
x>1时,f(x)>f(1),从而x2+5x-6>7lnx,得到
>1,通过整理变形不等式得证.
| 7 |
| x |
| 7 |
| 2x |
| 7 |
| 2x |
| 7 |
| 2x |
| 5 |
| 2 |
(II)由b=
| 4 |
| 7 |
| 2x2+2ax-4a2 |
| x |
| 2(x-a)(x+2a) |
| x |
当a=0时,f(x)的增区间为(0,+∞)当a>0时,f(x)的减区间为(0,a)增区间为(a,+∞)当a<0时,f(x)的减区间为(0,-2a)增区间为(-2a,+∞);
(Ⅲ) 由(Ⅰ)知,当a=
| 5 |
| 2 |
| 5 |
| 2 |
x>1时,f(x)>f(1),从而x2+5x-6>7lnx,得到
| n+1 |
| n |
解答:
解(Ⅰ)∵b=1,故f(x)=(x+a)2-7lnx+1,
∴f′(x)=2x+2a-
.
∵当x>1时,f(x)是增函数,
∴f′(x)=2x+2a-
≥0在x>1时恒成立.
即a≥
-x在x>1时恒成立.
∵当x>1时,y=
-x是减函数,
∴当x>1时,
-x<
,
∴a≥
.
(II)∵b=
a2,故f(x)=(x+a)2-4a2lnx+1,x∈(0,+∞),
∴f′(x)=
=
,
∴当a=0时,f(x)的增区间为(0,+∞)
当a>0时,∴f'(x)>0⇒x>a或x<-2a,
∴f(x)的减区间为(0,a),增区间为(a,+∞)
当a<0时,∴f'(x)>0⇒x>-2a或x<a,
∴f(x)的减区间为(0,-2a),增区间为(-2a,+∞);
(Ⅲ) 由(Ⅰ)知,
当a=
时,
f(x)=(x+
)2-7lnx+1在(1,+∞)是增函数.
∴当x>1时,f(x)>f(1),
即(x+
)2-7lnx+1>
,
∴x2+5x-6>7lnx
∵n∈N*,∴
>1,
∴(1+
)2+5(1+
)-6>7ln
,
即
+7
>7[ln(n+1)-lnn],
∴(
+
)+(
+
)…(
+
)>
7[ln2-ln1+ln3-ln2+…+ln(n+1)-lnn]
=7ln(n+1),
∴ln(n+1)7<(1+
+…+
)+7(1+
+…+
).
∴f′(x)=2x+2a-
| 7 |
| x |
∵当x>1时,f(x)是增函数,
∴f′(x)=2x+2a-
| 7 |
| x |
即a≥
| 7 |
| 2x |
∵当x>1时,y=
| 7 |
| 2x |
∴当x>1时,
| 7 |
| 2x |
| 5 |
| 2 |
∴a≥
| 5 |
| 2 |
(II)∵b=
| 4 |
| 7 |
∴f′(x)=
| 2x2+2ax-4a2 |
| x |
| 2(x-a)(x+2a) |
| x |
∴当a=0时,f(x)的增区间为(0,+∞)
当a>0时,∴f'(x)>0⇒x>a或x<-2a,
∴f(x)的减区间为(0,a),增区间为(a,+∞)
当a<0时,∴f'(x)>0⇒x>-2a或x<a,
∴f(x)的减区间为(0,-2a),增区间为(-2a,+∞);
(Ⅲ) 由(Ⅰ)知,
当a=
| 5 |
| 2 |
f(x)=(x+
| 5 |
| 2 |
∴当x>1时,f(x)>f(1),
即(x+
| 5 |
| 2 |
| 53 |
| 4 |
∴x2+5x-6>7lnx
∵n∈N*,∴
| n+1 |
| n |
∴(1+
| 1 |
| n |
| 1 |
| n |
| n+1 |
| n |
即
| 1 |
| n2 |
| 1 |
| n |
∴(
| 1 |
| 12 |
| 7 |
| 1 |
| 1 |
| 22 |
| 7 |
| 2 |
| 1 |
| n2 |
| 7 |
| n |
7[ln2-ln1+ln3-ln2+…+ln(n+1)-lnn]
=7ln(n+1),
∴ln(n+1)7<(1+
| 1 |
| 22 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| n |
点评:本题考察了利用导数求函数的单调性,求参数的取值范围,不等式的证明,是一道综合题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
“1≤x≤3”是“x2-2x-3≤0”的成立的什么条件?答( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
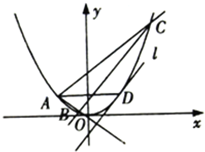 已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行
已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行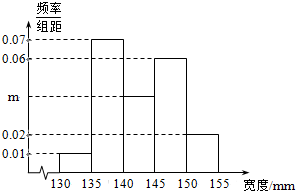 1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.
1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.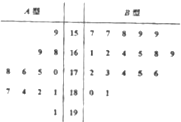 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”