题目内容
设直线nx+(n+1)y=
(n∈N*)与两坐标轴围成的三角形的面积为Sn,则S1+S2+…+S2014的值为 .
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,等差数列与等比数列
分析:由题意,求出Sn=
•
•
=
-
,即可求出S1+S2+…+S2014的值.
| 1 |
| 2 |
| ||
| n+1 |
| ||
| n |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:∵直线nx+(n+1)y=
,
∴y=-
x+
,
∴直线与两坐标轴的交点为(0,
),(
,0),
∴Sn=
•
•
=
-
;
∴S1+S2+S3+…+S2014=1-
+
-
+…+
-
=
.
故答案为:
.
| 2 |
∴y=-
| n |
| n+1 |
| ||
| n+1 |
∴直线与两坐标轴的交点为(0,
| ||
| n+1 |
| ||
| n |
∴Sn=
| 1 |
| 2 |
| ||
| n+1 |
| ||
| n |
| 1 |
| n |
| 1 |
| n+1 |
∴S1+S2+S3+…+S2014=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
故答案为:
| 2014 |
| 2015 |
点评:本题考查的是一次函数图象上点的坐标特点,根据题意找出规律是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若复数z为纯虚数,|z+|z||=
,则z=( )
| 2 |
| A、i | B、-i | C、±i | D、±2i |
设集合M={x|y=
,x∈R},集合N={y|y=x2,x∈R},则M∩N=( )
| x-2 |
| A、∅ | B、N | C、[0,+∞) | D、M |
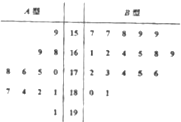 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”