题目内容
已知在△ABC中,角A、B、C的对边分别为a,b,c,且满足条件:a(sinA-sinC)+csinC=bsinB.
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=sinx•cos(x+B)+
(x∈[0,
])的值域.
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=sinx•cos(x+B)+
| ||
| 4 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,余弦定理
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)△ABC中,由正弦定理和余弦定理,求出cosB,即得B的值;
(Ⅱ)利用三角恒等变换,把f(x)化为
sin(2x+
),求出2x+
的取值范围,得出f(x)的值域.
(Ⅱ)利用三角恒等变换,把f(x)化为
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
解答:
解:(Ⅰ)△ABC中,∵a(sinA-sinC)+csinC=bsinB,
∴a(a-c)+c2=b2,
即a2+c2-b2=ac;
∴cosB=
=
,
∴B=
;
(Ⅱ)∵f(x)=sinx•cos(x+
)+
=
sinxcosx-
sin2x+
=
sin2x+
cos2x
=
sin(2x+
),
∵x∈[0,
],
∴2x+
∈[
,
],
∴-
≤sin(2x+
)≤1;
∴f(x)的值域为[-
,
].
∴a(a-c)+c2=b2,
即a2+c2-b2=ac;
∴cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴B=
| π |
| 3 |
(Ⅱ)∵f(x)=sinx•cos(x+
| π |
| 3 |
| ||
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴f(x)的值域为[-
| ||
| 4 |
| 1 |
| 2 |
点评:本题考查了正弦、余弦定理的应用问题以及三角恒等变换问题,解题时应根据三角恒等变换公式和正弦、余弦定理进行解答,是综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C:x+(y-1)2=
直线l:y=
x将l绕原点按逆时针方向旋转θ(θ为锐角)第一次与圆C相切,则tanθ的值是( )
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示:
某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示: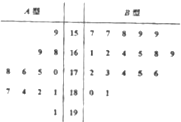 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”