题目内容
已知函数f(x)=
sin2x-cos2x-
(x∈R)
(1)求函数f(x)的最小值和最小值时x的集合;
(2)设△ABC的内角A,B,C对边分别为a,b,c,且c=
,f(C)=0,若
=(1,sinA)与
=(2,sinB)共线,求a,b的值.
| ||
| 2 |
| 1 |
| 2 |
(1)求函数f(x)的最小值和最小值时x的集合;
(2)设△ABC的内角A,B,C对边分别为a,b,c,且c=
| 3 |
| m |
| n |
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的图像与性质
分析:(1)首先,化简函数解析式f(x)=sin(2x-
)-1,然后,借助于三角函数的图象与性质求解最值即可;
(2)根据f(C)=sin(2C-
)-1=0,求解C=
,然后,根据余弦定理和坐标运算求解.
| π |
| 6 |
(2)根据f(C)=sin(2C-
| π |
| 6 |
| π |
| 3 |
解答:
解:(1)∵f(x)=
sin2x-cos2x-
=
sin2x-
-
=sin(2x-
)-1,
∴f(x)=sin(2x-
)-1,
∴函数f(x)的最小值为-2,当且仅当x=kπ+
,k∈Z,时取得,
最小值时x的集合{x|x=kπ+
,k∈Z,}.
(2)∵f(C)=sin(2C-
)-1=0,
∴sin(2C-
)=1,
∵0<C<π,
∴-
<2C-
<
,
∴2C-
=
,
∴C=
,
∵
=(1,sinA),与
=(2,sinB)共线,
∴
=
=
,①
∵c2=a2+b2-2abcos
=a2+b2-ab=3,②
∴联立①②,解得
a=1,b=2.
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
∴f(x)=sin(2x-
| π |
| 6 |
∴函数f(x)的最小值为-2,当且仅当x=kπ+
| 5π |
| 6 |
最小值时x的集合{x|x=kπ+
| 5π |
| 6 |
(2)∵f(C)=sin(2C-
| π |
| 6 |
∴sin(2C-
| π |
| 6 |
∵0<C<π,
∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴2C-
| π |
| 6 |
| π |
| 2 |
∴C=
| π |
| 3 |
∵
| m |
| n |
∴
| 1 |
| 2 |
| sinA |
| sinB |
| a |
| b |
∵c2=a2+b2-2abcos
| π |
| 3 |
∴联立①②,解得
a=1,b=2.
点评:本题重点考查了三角恒等变换公式、三角函数的性质、平面向量的坐标运算等知识,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在?ABCD中,错误的式子是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
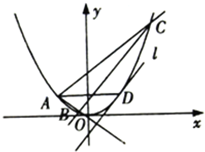 已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行
已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行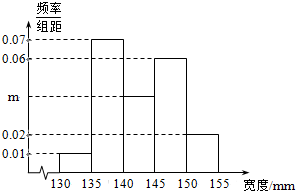 1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.
1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.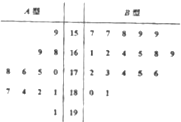 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”