题目内容
有11个座位,现安排甲、乙2人就坐,甲、乙都不坐正中间的1个座位,并且这两人不相邻的概率是 .
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:利用排列数公式求得11个座位,安排甲、乙2人就坐的座法种数,再利用间接法求符合条件的座法种数,即11个座位去掉中间的一个座位,甲、乙任意座的座法种数减去甲、乙相邻的情况,
代入古典概型概率公式计算.
代入古典概型概率公式计算.
解答:
解:11个座位,安排甲、乙2人就坐,共有
=11×10=110种座法;
其中甲、乙都不坐正中间的1个座位,且又不相邻的座法,用间接法计算如下,
11个座位去掉中间的一个座位,甲、乙任意座有
=90种座法,
把这两个捆绑在一起作为一个元素,甲、乙相邻的有
×
=18种座法,
又甲乙坐第5第7时不算邻坐,
∴甲、乙都不坐正中间的1个座位,且又不相邻的座法有90-18+2=74种座法,
∴甲、乙都不坐正中间的1个座位,且又不相邻的概率为
=
.
故答案为:
.
| A | 2 11 |
其中甲、乙都不坐正中间的1个座位,且又不相邻的座法,用间接法计算如下,
11个座位去掉中间的一个座位,甲、乙任意座有
| A | 2 10 |
把这两个捆绑在一起作为一个元素,甲、乙相邻的有
| A | 2 2 |
| C | 1 9 |
又甲乙坐第5第7时不算邻坐,
∴甲、乙都不坐正中间的1个座位,且又不相邻的座法有90-18+2=74种座法,
∴甲、乙都不坐正中间的1个座位,且又不相邻的概率为
| 74 |
| 110 |
| 37 |
| 55 |
故答案为:
| 37 |
| 55 |
点评:本题借助考查古典概型的概率计算考查了排列组合的应用,利用间接法求符合条件的座法种数是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若复数z为纯虚数,|z+|z||=
,则z=( )
| 2 |
| A、i | B、-i | C、±i | D、±2i |
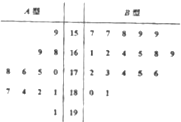 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”