题目内容
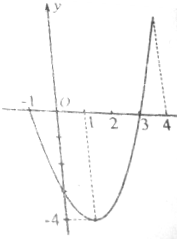
根据如图信息，求这个二次函数的值域．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据图象，函数的图象经过点（-1，0），（3，0），（1，-4），设二次函数的解析式为y=a（x+1）（x-3），代入解得即可
解答：
解：由图可知，函数的图象经过点（-1，0），（3，0），（1，-4），
设二次函数的解析式为y=a（x+1）（x-3），a＞0，
∴-4=a（1+1）（1-3），
解得a=1，
∴函数的解析式为y=（x+1）（x-3）=x2-2x-3，
当x=4时，y=42-2×4-3=5，
故函数的值域为[-4，5]．
设二次函数的解析式为y=a（x+1）（x-3），a＞0，
∴-4=a（1+1）（1-3），
解得a=1，
∴函数的解析式为y=（x+1）（x-3）=x2-2x-3，
当x=4时，y=42-2×4-3=5，
故函数的值域为[-4，5]．
点评：本题考查了二次函数的凸显和性质，以及解析式的求法，属于基础题
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
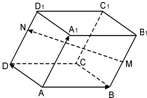如图的平行六面体ABCD-A1B1C1D1中，点M在BB1上，点N在DD1上，且BM=| 1 |
| 2 |
| 1 |
| 3 |
| MN |
| AB |
| AD |
| AA1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知抛物线y=ax2+bx+c（a≠0）的对称轴在y轴的左侧，其中a，b，c∈{-3，-2，-1，0，1，2，3}，在这些抛物线中，若随机变量X=a-b，则X的数学期望E（X）等于（ ）
A、
| ||
B、
| ||
C、
| ||
| D、0 |
已知
=
，则sin2α+cos（α-
）等于（ ）
| cos2α |
| cosα[1+tan(-α)] |
| ||
| 3 |
| π |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|