题目内容
已知⊙M:x2+y2-4x-8y+16=0,直线l:(1+λ)x+(1-λ)y-6=0(λ∈R).
(Ⅰ)求证:对任意λ∈R,都有直线l与⊙M相交;
(Ⅱ)当λ=2时,求直线l被⊙M截得的弦长;
(Ⅲ)已知点N(3,1),在⊙M内(包括圆周)任取一点P,记事件K为“点P与点N(3,1)所确定的直线到点M的距离不大于1”,求事件K发生的概率.
(Ⅰ)求证:对任意λ∈R,都有直线l与⊙M相交;
(Ⅱ)当λ=2时,求直线l被⊙M截得的弦长;
(Ⅲ)已知点N(3,1),在⊙M内(包括圆周)任取一点P,记事件K为“点P与点N(3,1)所确定的直线到点M的距离不大于1”,求事件K发生的概率.
考点:直线与圆的位置关系,几何概型
专题:综合题,直线与圆,概率与统计
分析:(Ⅰ)直线l:(1+λ)x+(1-λ)y-6=0可化为(x+y-6)+λ(x-y)=0,可得
,即可得出结论;
(Ⅱ)当λ=2时,求出圆心M到直线l的距离,即可求直线l被⊙M截得的弦长;
(Ⅲ)求出S弓形AB=S弓形CD=
-
×2×2sin
=
-
,S曲多边形ABDC=4π-2(
-
)=
+2
,由题意,P落在曲多边形ABDC内(包括边界)时满足题意,即可求出事件K发生的概率.
|
(Ⅱ)当λ=2时,求出圆心M到直线l的距离,即可求直线l被⊙M截得的弦长;
(Ⅲ)求出S弓形AB=S弓形CD=
| 4π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |
解答:
(Ⅰ)证明:直线l:(1+λ)x+(1-λ)y-6=0可化为(x+y-6)+λ(x-y)=0,
∴
,∴x=y=3,
(3,3)代入x2+y2-4x-8y+16=9+9-36-24+16=-46<0
∴对任意λ∈R,都有直线l与⊙M相交;
(Ⅱ)解:⊙M:x2+y2-4x-8y+16=0,可化为(x-2)2+(y-4)2=4,圆心M(2,4),半径为2
当λ=2时,直线l:3x-y-6=0,
圆心M到直线l的距离d=
=
,
∴直线l被⊙M截得的弦长为2
=
;
(Ⅲ)解:点N(3,1)在⊙M外,设过点N且与圆心的距离为1的两条直线NB和ND与⊙M分别交于A、B和C、D,
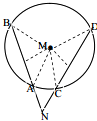
由于|MA|=|MB|=|MC|=|MD|=2,∴△MAB△MCD,∠AMB=∠CMD=
,
∴S弓形AB=S弓形CD=
-
×2×2sin
=
-
,
∴S曲多边形ABDC=4π-2(
-
)=
+2
,
由题意,P落在曲多边形ABDC内(包括边界)时满足题意,事件K发生的概率为(
+2
)÷4π=
.
∴
|
(3,3)代入x2+y2-4x-8y+16=9+9-36-24+16=-46<0
∴对任意λ∈R,都有直线l与⊙M相交;
(Ⅱ)解:⊙M:x2+y2-4x-8y+16=0,可化为(x-2)2+(y-4)2=4,圆心M(2,4),半径为2
当λ=2时,直线l:3x-y-6=0,
圆心M到直线l的距离d=
| |3×2-4-6| | ||
|
2
| ||
| 5 |
∴直线l被⊙M截得的弦长为2
22-(
|
4
| ||
| 5 |
(Ⅲ)解:点N(3,1)在⊙M外,设过点N且与圆心的距离为1的两条直线NB和ND与⊙M分别交于A、B和C、D,

由于|MA|=|MB|=|MC|=|MD|=2,∴△MAB△MCD,∠AMB=∠CMD=
| 2π |
| 3 |
∴S弓形AB=S弓形CD=
| 4π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 4π |
| 3 |
| 3 |
∴S曲多边形ABDC=4π-2(
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |
由题意,P落在曲多边形ABDC内(包括边界)时满足题意,事件K发生的概率为(
| 4π |
| 3 |
| 3 |
4π+6
| ||
| 12π |
点评:本题考查直线与圆的位置关系,考查几何概型,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
某足够大的长方体箱子内放置一球O,已知球O与长方体一个顶点出发的三个平面都相切,且球面上一点M到三个平面的距离分别为3,2,1,则此半球的半径为( )
A、3+2
| ||||
B、3-
| ||||
C、3+
| ||||
D、3+2
|
若变量x,y满足条件
,则x+2y的最小值为( )
|
A、-
| ||
| B、0 | ||
C、
| ||
D、
|