题目内容
已知单调递增的等差数列{an}满足a1=2,且a1,a2,a4成等比数列,其前n项和为Sn.
(Ⅰ)求数列{an}的通项公式及Sn;
(Ⅱ)设bn=
,求数列{
}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式及Sn;
(Ⅱ)设bn=
| Sn |
| n |
| 1 |
| bn•bn+1 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差为d(d>0),由已知结合a1,a2,a4成等比数列求得等差数列的公差,则等差数列的通项公式和前n项和公式可求;
(Ⅱ)把等差数列的前n项和代入bn=
,整理后代入
,然后利用裂项相消法求数列的和.
(Ⅱ)把等差数列的前n项和代入bn=
| Sn |
| n |
| 1 |
| bn•bn+1 |
解答:
解:(Ⅰ)设等差数列{an}的公差为d(d>0),
由a1=2,且a1,a2,a4成等比数列,得
(2+d)2=2(2+3d),解得:d=2.
∴an=2+2(n-1)=2n,
Sn=2n+
=n2+n;
(Ⅱ)由bn=
=
=n+1,
∴
=
=
-
,
则Tn=(
-
)+(
-
)+…+(
-
)
=
-
=
=
.
由a1=2,且a1,a2,a4成等比数列,得
(2+d)2=2(2+3d),解得:d=2.
∴an=2+2(n-1)=2n,
Sn=2n+
| 2n(n-1) |
| 2 |
(Ⅱ)由bn=
| Sn |
| n |
| n2+n |
| n |
∴
| 1 |
| bn•bn+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
则Tn=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
| n+2-2 |
| 2(n+2) |
| n |
| 2n+4 |
点评:本题考查了等差数列的通项公式,考查了等比数列的性质,训练了裂项相消法求数列的前n项和,是中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列结论正确的是( )
A、若向量
| ||||||||||||
B、已知向量
| ||||||||||||
| C、命题:若x2=1,则x=1或x=-1,故当x≥1的逆否命题为:若x≠1且x≠-1,则x2≠1 | ||||||||||||
| D、若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1>0 |
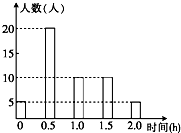 某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为