题目内容
数学归纳法证明：1+2+3+…+2n=n（2n+1）
考点：数学归纳法
专题：证明题,点列、递归数列与数学归纳法
分析：首先证明当n=1时等式成立，再假设n=k时等式成立，得到等式1+2+3+…+2k=k（2k+1），下面证明当n=k+1时等式左边=1+2+…+（2k+1）+（2k+2），根据前面的假设化简即可得到结果，最后得到结论．
解答：
证明：1°当n=1时的左边等于1+2=3，右边=1×3=3，结论成立；
2°设n=k时，结论成立，即1+2+3+…+2k=k（2k+1）成立．
当n=k+1时，左边=1+2+…+（2k+1）+（2k+2）=k（2k+1）+（2k+1）+（2k+2）=（k+1）[2（k+1）+1]，
于是当n=k+1时等式也成立．
综上，对任意自然数n∈N*等式成立
2°设n=k时，结论成立，即1+2+3+…+2k=k（2k+1）成立．
当n=k+1时，左边=1+2+…+（2k+1）+（2k+2）=k（2k+1）+（2k+1）+（2k+2）=（k+1）[2（k+1）+1]，
于是当n=k+1时等式也成立．
综上，对任意自然数n∈N*等式成立
点评：本题考查用数学归纳法证明等式成立，用数学归纳法证明问题的步骤是：第一步验证当n=n0时命题成立，第二步假设当n=k时命题成立，那么再证明当n=k+1时命题也成立．本题解题的关键是利用第二步假设中结论证明当n=k+1时成立，本题是一个中档题目．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
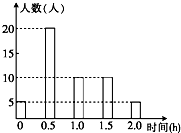某校为了了解学生的课外阅读情况，随机抽查了50名学生，得到他们某一天各自课外阅读的时间数据如图所示，根据条形图可得到这50名学生该天每人的平均课外阅读时间为
已知向量
=（{1，
），
=（3，m），若向量
与
的夹角为
，则实数m的值为（ ）
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
A、2
| ||
B、
| ||
| C、0 | ||
D、-
|