题目内容
已知直线l:y=ax+1-a(a∈R),曲线C:y=x2.问是否存在实数a,使得曲线C与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|.
考点:二次函数的性质
专题:函数的性质及应用
分析:联立直线l的方程和曲线C的方程可求出直线l和曲线C的交点为(1,1),(a-1,(a-1)2),所以根据已知条件及两点间距离公式可得到
=|a|.两边平方可得(a-2)2+(a2-2a)2-a2=0 ①,设f(a)=(a-2)2+(a2-2a)2-a2,容易求得f(0)>0,f(2)<0,所以f(a)在(0,2)上有零点,即方程①有实数根,所以说存在实数a,使得曲线C与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|.
| (a-2)2+(a2-2a)2 |
解答:
解:由
得,x2-ax+a-1=[x-(a-1)](x-1)=0;
∴x=1,或a-1;
∴直线l和曲线C的交点为(1,1),(a-1,(a-1)2);
∴
=|a|;
(a-2)2+(a2-2a)2-a2=0;
设f(a)=(a-2)2+(a2-2a)2-a2;
f(0)=4>0,f(2)=-4<0,且f(a)是连续函数;
∴f(a)在(0,2)上有零点;
即方程(a-2)2+(a2-2a)2-a2=0在(0,2)上有根,并且在a∈(0,2)上曲线C和直线l有两个不同交点;
即存在实数a,使得曲线C与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|.
|
∴x=1,或a-1;
∴直线l和曲线C的交点为(1,1),(a-1,(a-1)2);
∴
| (a-2)2+(a2-2a)2 |
(a-2)2+(a2-2a)2-a2=0;
设f(a)=(a-2)2+(a2-2a)2-a2;
f(0)=4>0,f(2)=-4<0,且f(a)是连续函数;
∴f(a)在(0,2)上有零点;
即方程(a-2)2+(a2-2a)2-a2=0在(0,2)上有根,并且在a∈(0,2)上曲线C和直线l有两个不同交点;
即存在实数a,使得曲线C与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|.
点评:考查联立直线方程和曲线方程求直线和曲线交点坐标的方法,解一元二次方程,两点间距离公式,以及函数零点的概念及判断零点是否存在的方法.

练习册系列答案
相关题目
点O在△ABC的内部,且满足
+2
+4
=0,则△ABC的面积与△AOC的面积之比是( )
| OA |
| OB |
| OC |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
已知数列{an}的前n项和为Sn,a1=1,当n≥2时,an+2Sn-1=n,则S2015的值为( )
| A、2015 | B、2013 |
| C、1008 | D、1007 |
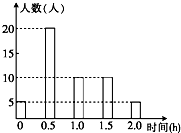 某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为