题目内容
已知数列{an}是等比数列,且a1+a2+a3=-6,且a1•a2•a3=64,(|q|>1)
(1)求{an}的通项公式;
(2)令bn=(2n+1)•an,求数列{bn}的前n项和的公式.
(1)求{an}的通项公式;
(2)令bn=(2n+1)•an,求数列{bn}的前n项和的公式.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)设数列{an}的公比为q,可得a1=
,从而可求得q=-2,a1=-2,故可求{an}的通项公式;
(2)bn=(2n+1)(-2)n,可得Sn=b1+b2+b3+…+bn=3×(-2)+5×(-2)2+7×(-2)3+9×(-2)2+…+(2n+1)(-2)n ,利用错误相加法可得Sn.
| 4 |
| q |
(2)bn=(2n+1)(-2)n,可得Sn=b1+b2+b3+…+bn=3×(-2)+5×(-2)2+7×(-2)3+9×(-2)2+…+(2n+1)(-2)n ,利用错误相加法可得Sn.
解答:
解:(1)设数列{an}的公比为q,则有
a1(1+q+q2)=-6 ①
a13×q3=64 ②
由②式可得a1=
代入①式
可得q=-2或者-
(|q|>1故舍去)
所以求得a1=-2.
故{an}的通项公式an=a1qn-1=(-2)n.
(2)bn=(2n+1)•an=(2n+1)(-2)n
Sn=b1+b2+b3+…+bn=3×(-2)+5×(-2)2+7×(-2)3+9×(-2)2+…+(2n+1)(-2)n …③
(-2)×Sn=3×(-2)2+5×(-2)3+7×(-2)4+9×(-2)5+…+(2n+1)(-2)n+1…④
③-④得
3Sn=3×(-2)+2×(-2)2+2×(-2)3+2×(-2)4+2×(-2)5+…+2×(-2)n-(2n+1)(-2)n+1
=-6+2×[(-2)2+(-2)3+(-2)4+(-2)5+…(-2)n]-(2n+1)(-2)n+1
=-6+2×
-(2n+1)(-2)n+1
=-
-
-
=-
-
故Sn=-
-
.
a1(1+q+q2)=-6 ①
a13×q3=64 ②
由②式可得a1=
| 4 |
| q |
可得q=-2或者-
| 1 |
| 2 |
所以求得a1=-2.
故{an}的通项公式an=a1qn-1=(-2)n.
(2)bn=(2n+1)•an=(2n+1)(-2)n
Sn=b1+b2+b3+…+bn=3×(-2)+5×(-2)2+7×(-2)3+9×(-2)2+…+(2n+1)(-2)n …③
(-2)×Sn=3×(-2)2+5×(-2)3+7×(-2)4+9×(-2)5+…+(2n+1)(-2)n+1…④
③-④得
3Sn=3×(-2)+2×(-2)2+2×(-2)3+2×(-2)4+2×(-2)5+…+2×(-2)n-(2n+1)(-2)n+1
=-6+2×[(-2)2+(-2)3+(-2)4+(-2)5+…(-2)n]-(2n+1)(-2)n+1
=-6+2×
| 4(1-(-2)n-1) |
| 1+2 |
=-
| 10 |
| 9 |
| 8(-2)n-1 |
| 9 |
| (2n+1)(-2)n+1 |
| 3 |
=-
| 10 |
| 9 |
| (6n+5)(-2)n+1 |
| 9 |
故Sn=-
| 10 |
| 9 |
| (6n+5)(-2)n+1 |
| 9 |
点评:本题主要考察了等差数列与等比数列的综合应用,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
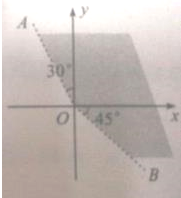 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是