题目内容
已知集合A={y|y=-2x,x∈[2,3]},B={x|x2+3x-a2-3a>0}.
(1)当a=4时,求A∩B;
(2)若命题“x∈A”是命题“x∈B”的充分不必要条件,求实数a的取值范围.
(1)当a=4时,求A∩B;
(2)若命题“x∈A”是命题“x∈B”的充分不必要条件,求实数a的取值范围.
考点:交集及其运算,必要条件、充分条件与充要条件的判断
专题:集合
分析:(1)求出集合A,B的元素,利用集合的基本运算即可得到结论.
(2)根据充分条件和必要条件的定义结合集合之间的关系即可得到结论.
(2)根据充分条件和必要条件的定义结合集合之间的关系即可得到结论.
解答:
解:(1)当a=4时,B={x|x2+3x-a2-3a>0}={x|x2+3x-28>0}={x|x>4或x<-7}.
A={y|y=-2x,x∈[2,3]}={y|-8<y<-4},
则A∩B={x|-8<x<-7}.
(2)若命题“x∈A”是命题“x∈B”的充分不必要条件,则A⊆B,
B={x|x2+3x-a2-3a>0}={x|(x-a)(x+a+3)>0}.
对应方程的两个根为x=a或x=-a-3,
①若a=-a-3,即a=-
,此时B={x|x≠-
},满足A⊆B,
②若a<-a-3,即a<-
,此时B={x|x>-a-3或x<a}},
若满足A⊆B,则a>-4或-a-3<-8,解得a>-4或a>5(舍去),
此时-1<a<-
.
③若a>-a-3,即a>-
,此时B={x|x>a或x<-a-3}},
若满足A⊆B,则-a-3>-4或a<-8(舍),解得-
<a<1.
综上-4<a<1.
A={y|y=-2x,x∈[2,3]}={y|-8<y<-4},
则A∩B={x|-8<x<-7}.
(2)若命题“x∈A”是命题“x∈B”的充分不必要条件,则A⊆B,
B={x|x2+3x-a2-3a>0}={x|(x-a)(x+a+3)>0}.
对应方程的两个根为x=a或x=-a-3,
①若a=-a-3,即a=-
| 3 |
| 2 |
| 3 |
| 2 |
②若a<-a-3,即a<-
| 3 |
| 2 |
若满足A⊆B,则a>-4或-a-3<-8,解得a>-4或a>5(舍去),
此时-1<a<-
| 3 |
| 2 |
③若a>-a-3,即a>-
| 3 |
| 2 |
若满足A⊆B,则-a-3>-4或a<-8(舍),解得-
| 3 |
| 2 |
综上-4<a<1.
点评:本题主要考查集合的基本运算以及充分条件和必要条件的应用,注意要进行分类讨论.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有( )
| A、30 | B、20 | C、10 | D、6 |
已知一组数据a1,a2,a3,…,an的平均数为
,标准差为s,则-2a1+3,-2a2+3,-2a3+3,…,-2an+3的平均数和标准差分别是( )
. |
| x |
A、
| ||
B、-2
| ||
C、-2
| ||
D、-2
|

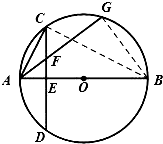 已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.
已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.