题目内容
下列命题:
①(
)2•(
)2=|
|4;
②(
•
)•
=(
•
)•
;
③|
•
|=|
|•|
|;
④若
∥
,
∥
,则
∥
;
⑤
∥
,则存在唯一实数λ,使
=λ
;
⑥若
•
=
•
,且
≠
,则
=
;
⑦设
,
是平面内两向量,则对于平面内任何一向量
,都存在唯一一组实数x、y,使
=x
+y
成立;
⑧若
•
=0,则
=
或
=
.
真命题的题号为 .
①(
| a |
| a |
| a |
②(
| a |
| b |
| c |
| a |
| c |
| b |
③|
| a |
| b |
| a |
| b |
④若
| a |
| b |
| b |
| c |
| a |
| c |
⑤
| a |
| b |
| b |
| a |
⑥若
| a |
| c |
| b |
| c |
| c |
| 0 |
| a |
| b |
⑦设
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
⑧若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
真命题的题号为
考点:函数奇偶性的判断
专题:平面向量及应用
分析:根据数量积的计算公式,共线向量基本定理,以及平面向量基本定理即可找出真命题.
解答:
解:①正确,根据数量积的计算公式即可得出;
②错误,(
•
)•
是向量,并且与
共线,(
•
)•
是向量,与
共线,而
,
不一定共线;
③错误,|
•
|=||
||
|cosθ|=|
||
||cosθ|,而|cosθ|不一定为1;
④正确,根据向量的几何意义即可得出;
⑤错误,若
=
时,λ便不唯一了;
⑥错误,由
•
=
•
得|
||
|cosθ1=|
||
|cosθ2,所以得到|
|cosθ1=|
|cosθ2;
显然|
|不一定等于|
|,所以
≠
;
⑦错误,若
∥
,而
不与
,
共线,则不存在实数x,y使
=x
+y
;
⑧错误,
•
=|
||
|cosθ=0,cosθ可能等于0,而|
|,|
|都不为0,即得不到
=
或
=
;
∴综上得为真命题的是①④.
故答案为:①④.
②错误,(
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| b |
| c |
| b |
③错误,|
| a |
| b |
| a |
| b |
| a |
| b |
④正确,根据向量的几何意义即可得出;
⑤错误,若
| a |
| 0 |
⑥错误,由
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
显然|
| a |
| b |
| a |
| b |
⑦错误,若
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
| e1 |
| e2 |
⑧错误,
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| 0 |
| b |
| 0 |
∴综上得为真命题的是①④.
故答案为:①④.
点评:考查数量积的运算公式,共线向量基本定理,以及共面向量基本定理.

练习册系列答案
相关题目
函数f(x)=
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
-2,e6+
-2)
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
|
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
| 1 |
| e |
| 1 |
| e2 |
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
已知一组数据a1,a2,a3,…,an的平均数为
,标准差为s,则-2a1+3,-2a2+3,-2a3+3,…,-2an+3的平均数和标准差分别是( )
. |
| x |
A、
| ||
B、-2
| ||
C、-2
| ||
D、-2
|
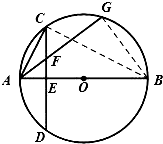 已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.
已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.