题目内容
已知函数f(x)=sinx,将函数f(x)图象上所有点的横坐标缩短为原来的
倍(纵坐标不变),得到函数g(x)的图象,则关于f(x)g(x)有下列命题,其中真命题的个数是( )
①函数y=f(x)•g(x)是偶函数;
②函数y=f(x)•g(x)是周期函数;
③函数y=f(x)•g(x)的图象关于点(
,0)中心对称;
④函数y=f(x)•g(x)的最大值为
.
| 1 |
| 2 |
①函数y=f(x)•g(x)是偶函数;
②函数y=f(x)•g(x)是周期函数;
③函数y=f(x)•g(x)的图象关于点(
| π |
| 2 |
④函数y=f(x)•g(x)的最大值为
4
| ||
| 9 |
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:综合题,导数的概念及应用,三角函数的图像与性质
分析:根据题意,求出y=f(x)•g(x)的解析式,判断:
①根据函数的奇偶性定义即可得出结论是否正确;
②根据周期函数的定义即可判断是否正确;
③根据f(
+x)•g(
+x)=-f(
-x)•g(
-x)得出函数y的图象关于点(
,0)中心对称;
④利用换元法求出y的最大值即可.
①根据函数的奇偶性定义即可得出结论是否正确;
②根据周期函数的定义即可判断是否正确;
③根据f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
④利用换元法求出y的最大值即可.
解答:
解:根据题意,∵f(x)=sinx,∴g(x)=sin2x,∴y=f(x)•g(x)=sinx•sin2x;
对于①,∵f(-x)•g(-x)=sin(-x)•sin2(-x)=(-sinx)•(-sin2x)=sinxsin2x=f(x)•g(x),
∴y=f(x)•g(x)是偶函数,①正确;
对于②,∵f(2π+x)•g(2π+x)=sin(2π+x)•sin(4π+2x)=sinx•sin2x=f(x)•g(x),
∴y=f(x)•g(x)是周期函数,②正确;
对于③,∵f(
+x)•g(
+x)=sin(
+x)sin(π+2x)=cosxsin2x
f(
-x)•g(
-x)=sin(
-x)sin(π-2x)=-cosxsin2x
∴f(
+x)•g(
+x)=-f(
-x)•g(
-x)
∴y=f(x)•g(x)的图象关于点(
,0)中心对称,③正确;
对于④,y=f(x)•g(x)=sinxsin2x=2sin2xcosx=2(1-cos2x)cosx,
设t=cosx,t∈[-1,1],
∴y=2t-2t3,求导得y′=2-6t2;
∴当t∈[-1,-
)时,y′<0,函数y是减函数,
当t∈(-
,
)时,y′>0,函数y是增函数,
当t∈(
,1]时,y′<0,函数y是减函数;
∴当t=
时,y取得最大值是ymax=2×
-2×(
)3=
,④正确;
综上,正确的命题是①②③④,4个.
故选:D.
对于①,∵f(-x)•g(-x)=sin(-x)•sin2(-x)=(-sinx)•(-sin2x)=sinxsin2x=f(x)•g(x),
∴y=f(x)•g(x)是偶函数,①正确;
对于②,∵f(2π+x)•g(2π+x)=sin(2π+x)•sin(4π+2x)=sinx•sin2x=f(x)•g(x),
∴y=f(x)•g(x)是周期函数,②正确;
对于③,∵f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴y=f(x)•g(x)的图象关于点(
| π |
| 2 |
对于④,y=f(x)•g(x)=sinxsin2x=2sin2xcosx=2(1-cos2x)cosx,
设t=cosx,t∈[-1,1],
∴y=2t-2t3,求导得y′=2-6t2;
∴当t∈[-1,-
| ||
| 3 |
当t∈(-
| ||
| 3 |
| ||
| 3 |
当t∈(
| ||
| 3 |
∴当t=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
4
| ||
| 9 |
综上,正确的命题是①②③④,4个.
故选:D.
点评:本题考查了三角函数的图象与性质的应用,也考查了导数的综合应用问题,是综合题.

练习册系列答案
相关题目
若集合A={x|x2-7x+10<0},集合B={x|
<2x<8},则A∩B=( )
| 1 |
| 2 |
| A、(-1,3) |
| B、(-1,5) |
| C、(2,5) |
| D、(2,3) |
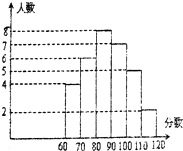 某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )
某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有( )
| A、30 | B、20 | C、10 | D、6 |