题目内容
(文科)设函数f(x)=
(a≠2).
(1)用反证法证明:函数f(x)不可能为偶函数;
(2)求证:函数f(x)在(-∞,-1)上单调递减的充要条件是a>2.
| 2x+a |
| x+1 |
(1)用反证法证明:函数f(x)不可能为偶函数;
(2)求证:函数f(x)在(-∞,-1)上单调递减的充要条件是a>2.
考点:必要条件、充分条件与充要条件的判断,反证法与放缩法
专题:函数的性质及应用,导数的综合应用
分析:(1)利用偶函数的性质和反证法即可得出;
(2)利用导数与函数单调性的关系、充分必要条件即可得出.
(2)利用导数与函数单调性的关系、充分必要条件即可得出.
解答:
(1)解:假设函数f(x)是偶函数,
则f(-2)=f(2),即
=
,解得a=2,
这与a≠2矛盾,
∴函数f(x)不可能是偶函数.
(2)证明:∵f(x)=
,(x≠-1).
∴f′(x)=
.
①充分性:当a>2时,f′(x)=
<0,
∴函数f(x)在(-∞,-1)单调递减;
②必要性:当函数f(x)在(-∞,-1)单调递减时,
有f′(x)=
≤0,即a≥2,又a≠2,∴a>2.
综合①②知,原命题成立.
则f(-2)=f(2),即
| -4+a |
| -1 |
| 4+a |
| 3 |
这与a≠2矛盾,
∴函数f(x)不可能是偶函数.
(2)证明:∵f(x)=
| 2x+a |
| x+1 |
∴f′(x)=
| 2-a |
| (x+1)2 |
①充分性:当a>2时,f′(x)=
| 2-a |
| (x+1)2 |
∴函数f(x)在(-∞,-1)单调递减;
②必要性:当函数f(x)在(-∞,-1)单调递减时,
有f′(x)=
| 2-a |
| (x+1)2 |
综合①②知,原命题成立.
点评:本题考查了偶函数的性质、反证法、利用导数研究函数单调性、充分必要条件等基础知识与基本技能方法,考查了推理能力和分类讨论的思想方法,属于难题.

练习册系列答案
相关题目
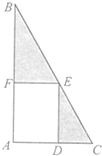 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=