题目内容
已知函数f(x)=ax+lnx,g(x)=a-aex
(1)若函数f(x)的图象在x=1处切线倾斜角为60°,求a的值;
(2)若对任意的x1,x2∈(0,+∞)均有f(x1)<g(x2),求a的取值范围.
(1)若函数f(x)的图象在x=1处切线倾斜角为60°,求a的值;
(2)若对任意的x1,x2∈(0,+∞)均有f(x1)<g(x2),求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由函数f(x)的图象在x=1处切线倾斜角为60°,可得f′(1)=tan60°.解出即可;
(2)x1,x2∈(0,+∞)均有f(x1)<g(x2)?f(x)max<g(x)min.通过对a分类讨论,利用导数可得函数f(x)的最大值,再利用指数函数的单调性可得g(x)的最小值.
(2)x1,x2∈(0,+∞)均有f(x1)<g(x2)?f(x)max<g(x)min.通过对a分类讨论,利用导数可得函数f(x)的最大值,再利用指数函数的单调性可得g(x)的最小值.
解答:
解:(1)f′(x)=a+
(x>0),
∵函数f(x)的图象在x=1处切线倾斜角为60°,∴f′(1)=tan60°.
即a+1=
.
∴a=
-1.
(2)x1,x2∈(0,+∞)均有f(x1)<g(x2)?f(x)max<g(x)min.
当a≥0时,f′(x)=a+
=
,
∵x>0,∴f′(x)=
>0,
∴f(x)在(0,+∞)上单调递增.
故f(x)在(0,+∞)上不存在最大值,
因此a≥0时不合题意.
当a<0时,f′(x)=
=0,得x=-
.
当x∈(0,-
)时,f(x)单调递增,当x∈(-
,+∞)时,f(x)单调递减,
故x∈(0,+∞)时,f(x)max=f(-
)=-1+ln(-
),
而当a<0时,g(x)=a-aex单调递增,g(x)>g(0)=0,
于时,f(x)max=f(-
)=-1+ln(-
)<0,解得a<-
.
| 1 |
| x |
∵函数f(x)的图象在x=1处切线倾斜角为60°,∴f′(1)=tan60°.
即a+1=
| 3 |
∴a=
| 3 |
(2)x1,x2∈(0,+∞)均有f(x1)<g(x2)?f(x)max<g(x)min.
当a≥0时,f′(x)=a+
| 1 |
| x |
| ax+1 |
| x |
∵x>0,∴f′(x)=
| ax+1 |
| x |
∴f(x)在(0,+∞)上单调递增.
故f(x)在(0,+∞)上不存在最大值,
因此a≥0时不合题意.
当a<0时,f′(x)=
| ax+1 |
| x |
| 1 |
| a |
当x∈(0,-
| 1 |
| a |
| 1 |
| a |
故x∈(0,+∞)时,f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
而当a<0时,g(x)=a-aex单调递增,g(x)>g(0)=0,
于时,f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
| 1 |
| e |
点评:本题考查了导数的几何意义、利用导数研究函数的单调性极值与最值、恒成立问题的等价转化方法等基础知识与基本技能方法,考查了推理能力和计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
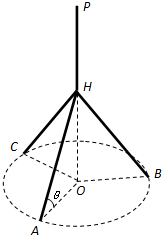 如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3
如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3