题目内容

求在极坐标系中，以（2，
π
2
）为圆心，2为半径的圆的参数方程．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：由极坐标易得圆心和半径，可得圆的标准方程，化为参数方程即可．
解答： 解：解：设点（2，
π
2
）在直角坐标系中的坐标为C（m，n），
可得m=2cos
π
2
=0，n=2sin
π
2
=2
∴C的直角坐标坐标为（0，2）
结合圆C的半径为R=2可得圆C的方程为x2+（y-2）2=4
化为参数方程可得：
x=2cosθ
y=2sinθ+2
（θ为参数）
点评：本题考查极坐标和参数方程，属基础题．
练习册系列答案
相关题目
已知函数f（x）=ax，g（x）=lnx，其中a为任意实数
（1）若函数F（x）=f（x）-g（x）有极值1，求a的值；
（2）若函数G（x）=f[sin（1-x）]+g（x）在区间（0，1）为增函数，求a的范围．
设函数f（x）=sinx（sinx+cosx）．
（Ⅰ）求f（
π
8
）的值；
（Ⅱ）若函数f（x）在[0，a]上的值域为[0，
1+
2
2
]，求实数a的取值范围．
以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴建立极坐标系．直线l的极坐标方程为pcosθ-psinθ+2=0，曲线C1的参数方程为
x=4cosθ
y=sinθ
（θ为参数），点M（x0，y0）在曲线C1上，动点P（x，y）其坐标满足
x=
1
4
x0
y=y0
．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）记动点P（x，y）的轨迹为曲线C2，试判断直线l与曲线C2的交点个数．
已知a=
2
1
为矩阵A=
1a
-14
属于特征值λ的一个特征向量．
（Ⅰ）求实数a，λ的值；       
（Ⅱ）求矩阵A的逆矩阵A-1．
（文科）设函数f（x）=
2x+a
x+1
（a≠2）．
（1）用反证法证明：函数f（x）不可能为偶函数；
（2）求证：函数f（x）在（-∞，-1）上单调递减的充要条件是a＞2．
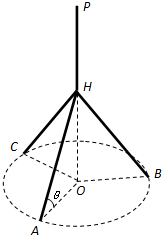如图所示，某人想制造一个支架，它由四根金属杆PH，HA，HB，HC构成，其底端三点A，B，C均匀地固定在半径为3m的圆O上（圆O在地面上），P，H，O三点相异且共线，PO与地面垂直．现要求点P到地面的距离恰为3
3
m，记用料总长为L=PH+HA+HB+HC，设∠HAO=θ．
（1）试将L表示为θ的函数，并注明定义域；
（2）当θ的正弦值是多少时，用料最省？
已知等差数列{an}的公差为d，若a1，a2，a3，a4，a5的方差为8，则d的值为
 
．
袋中有大小相同的白球4个，红球2个，从中不放回地任取2个，至少取到1个红球的概率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网