题目内容
已知抛物线y2=4x上一点P到焦点的距离等于2，并且点P在x轴下方，则点P的坐标是 ．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x的值，代入抛物线方程求得y值，即可得到所求点的坐标．
解答：
解：∵抛物线方程为y2=4x，
∴焦点为F（1，0），准线为l：x=-1
∵抛物线y2=4x上一点P到焦点的距离等于2，
∴根据抛物线定义可知P到准线的距离等于2，
即x+1=2，解之得x=1，
代入抛物线方程求得y=±2，
∵点P在x轴下方，
∴点P坐标为：（1，-2）
故答案为：（1，-2）．
∴焦点为F（1，0），准线为l：x=-1
∵抛物线y2=4x上一点P到焦点的距离等于2，
∴根据抛物线定义可知P到准线的距离等于2，
即x+1=2，解之得x=1，
代入抛物线方程求得y=±2，
∵点P在x轴下方，
∴点P坐标为：（1，-2）
故答案为：（1，-2）．
点评：本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决．
练习册系列答案
相关题目
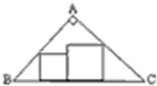从等腰直角三角形纸片ABC上，剪下如图所示的两个正方形，其中BC=4，∠A=90°，则这两个正方形的面积之和的最小值为由a1=1，d=3确定的等差数列{an}，当an=295时，序号n等于（ ）
| A、98 | B、99 | C、95 | D、100 |