题目内容
求值:(2cos
+1)?tan
-2sin
.
| π |
| 9 |
| 2π |
| 9 |
| π |
| 9 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:将所求关系式中的“切”化为“弦”,理由三角函数中的恒等变换应用,理由两角差的正弦及灵活的拆分角即可求得答案.
解答:
解:原式=
=
=
=
=
=
.
(2cos
| ||||||||
cos
|
=
2sin(
| ||||||
cos
|
=
2sin
| ||||
cos
|
=
2sin(
| ||||||
cos
|
=
2sin
| ||||
cos
|
| 3 |
点评:本题考查三角函数中的恒等变换应用,考查两角差的正弦,考查拆分角的技巧与运算求解能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,且a>b,则正确的是( )
| A、sinA>sinB且cosA>cosB |
| B、sinA<sinB且cosA<cosB |
| C、sinA>sinB且cosA<cosB |
| D、sinA<sinB且cosA>cosB |
一个直径为8cm的大金属球,熔化后铸成若干个直径为2cm的小球,如果不计损耗,可铸成小球的个数为( )
| A、4 | B、8 | C、16 | D、64 |
将6个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不同,则不同的放法共有( )
| A、4种 | B、6种 | C、8种 | D、10种 |
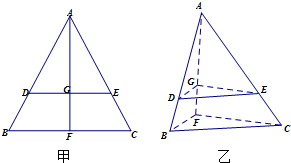 在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.
在等边三角形ABC中,D、E分别是AB、BC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF折起,得到如图乙所示的三棱锥A-BCF.