题目内容
17.(1)求值:$\frac{{sin{{330}^0}.sin(-\frac{13}{3}π).sin{{270}^0}}}{{cos(-\frac{19}{6}π).cos{{690}^0}}}$(2)已知角α终边上一点P(-4,3),求$\frac{cos(\frac{π}{2}+α)sin(-π-α)}{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}$的值.
分析 (1)利用诱导公式和特殊角的三角函数值进行化简;
(2)利用诱导公式对所求的代数式进行化简,然后代入求值.
解答 解:(1)原式=$\frac{-sin30°•(-sin\frac{π}{3})•(-sin90°)}{-cos\frac{π}{6}•cos30°}$=$\frac{{(-\frac{1}{2}).(-\frac{{\sqrt{3}}}{2}).(-1)}}{{(-\frac{{\sqrt{3}}}{2}).\frac{{\sqrt{3}}}{2}}}=\frac{{\sqrt{3}}}{3}$;
(2)∵角α终边上一点P(-4,3),
∴tanα=-$\frac{3}{4}$,
∴$\frac{cos(\frac{π}{2}+α)sin(-π-α)}{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}$
=$\frac{-sinα•sinα}{-sinα•cosα}$
=tanα
=-$\frac{3}{4}$.
点评 本题主要考察了同角三角函数关系式和诱导公式的应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知3是函数$f(x)=\left\{\begin{array}{l}{log_3}(x+t),x≥3\\{3^x},x<3\end{array}\right.$的一个零点,则f[f(6)]的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | log34 |
5.不等式ax2+bx+c<0的解集为空集,则( )
| A. | a<0,△>0 | B. | a<0,△≥0 | C. | a>0,△≤0 | D. | a>0,△≥0 |
9.已知$cos(\frac{3π}{14}-θ)=\frac{1}{3}$,则$sin(\frac{2π}{7}+θ)$=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
7.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若ac>bc,则a>b | C. | 若$\frac{1}{a}>\frac{1}{b},则a<b$ | D. | 若$\sqrt{a}<\sqrt{b},则a<b$ |

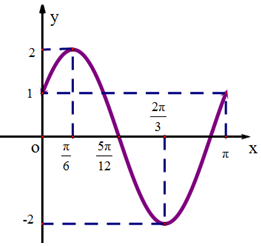 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.