题目内容
已知f(x)-2f(
)=3x-2,求f(x)的解析式.
| 1 |
| x |
考点:函数解析式的求解及常用方法
专题:方程思想,换元法,函数的性质及应用
分析:根据f(x)-2f(
)=3x-2,用
代替x,得出另一方程,解方程组,求出f(x)的解析式.
| 1 |
| x |
| 1 |
| x |
解答:
解:∵f(x)-2f(
)=3x-2…①,
∴f(
)-2f(x)=3•
-2…②,
②×2,得;
2f(
)-4f(x)=
-4…③,
③+①,得;
-3f(x)=3x+
-6,
∴f(x)=-x-
-2.
| 1 |
| x |
∴f(
| 1 |
| x |
| 1 |
| x |
②×2,得;
2f(
| 1 |
| x |
| 6 |
| x |
③+①,得;
-3f(x)=3x+
| 6 |
| x |
∴f(x)=-x-
| 2 |
| x |
点评:本题考查了利用方程组求函数解析式的应用问题,是基础题目.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设l、m是两条不同的直线,α,β是两个不同的平面,则下列命题为真命题的是( )
| A、若m∥l,m∥α,则l∥α |
| B、若m⊥α,l⊥m,则l∥α |
| C、若α∥β,l⊥α,m∥β,则l⊥m |
| D、若m?α,m∥β,l?β,l∥α,则α∥β |
若θ∈[0,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
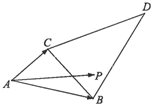
如图,△BCD与△ABC的面积之比为2,点P是区域ABCD内任意一点(含边界),且
=λ
+μ
(λ,μ∈R),则λ+μ的取值范围是( )
| AP |
| AB |
| AC |

| A、[0,1] |
| B、[0,2] |
| C、[0,3] |
| D、[0,4] |
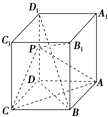 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点