题目内容
在△ABC中,A=
,AC=4,BC=2
,则ABC的面积等于 .
| π |
| 3 |
| 3 |
考点:正弦定理
专题:解三角形
分析:由正弦定理可得可求得sinB=
=
=1.由于B的范围可求B,从而可求C,由三角形面积公式即可得解.
| AC•sinA |
| BC |
4×sin
| ||
2
|
解答:
解:由正弦定理可得:
=
,从而有:sinB=
=
=1.
由于0<B<π,可得B=
,C=π-
-
=
故有:S△ABC=
AC•BC•sinC=2
.
故答案为:2
.
| AC |
| sinB |
| BC |
| sinA |
| AC•sinA |
| BC |
4×sin
| ||
2
|
由于0<B<π,可得B=
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
故有:S△ABC=
| 1 |
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题主要考查了正弦定理,三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
已知函数y=logax(a>0,a≠1)的图象经过点(2,
),则其反函数的解析式为( )
| 1 |
| 2 |
| A、y=4x | ||
| B、y=log4x | ||
| C、y=2x | ||
D、y=(
|
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log2x,则f(-8)值为( )
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
若复数Z1=1+i,Z2=3-i,则
=( )
| Z2 |
| Z1 |
| A、1+i | B、1+2i |
| C、1-2i | D、2-2i |
设函数f(x)=x3-22-x的零点为x0,则x0所在的大致区间是( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
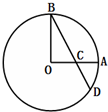 如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=
如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=