题目内容
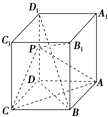 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点(1)求证:直线BD1∥平面PAC
(2)求证:直线PB1⊥平面PAC.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)直接利用三角形的中位线,得到线线平行,进一步利用线面平行的判定定理得到结论.
(2)利用线面垂直的判定和性质定理和勾股定理得逆定理得到线线垂直,进一步利用线面垂直的判定得到结论.
(2)利用线面垂直的判定和性质定理和勾股定理得逆定理得到线线垂直,进一步利用线面垂直的判定得到结论.
解答:
证明:(1)长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点
连接AC和BD,相较于O,连接OP,
所以:OP∥BD1
BD1?平面PAC,OP?平面PAC
所以:直线BD1∥平面PAC
(2)连接OB1,由于四边形ABCD是正方形,所以AC⊥BD
BB1⊥平面ABCD
所以:AC⊥平面BB1D1D
则:AC⊥PB1
由于:PB12+OP2=OB12
所以:PB1⊥OP
直线PB1⊥平面PAC
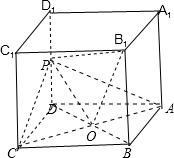
连接AC和BD,相较于O,连接OP,
所以:OP∥BD1
BD1?平面PAC,OP?平面PAC
所以:直线BD1∥平面PAC
(2)连接OB1,由于四边形ABCD是正方形,所以AC⊥BD
BB1⊥平面ABCD
所以:AC⊥平面BB1D1D
则:AC⊥PB1
由于:PB12+OP2=OB12
所以:PB1⊥OP
直线PB1⊥平面PAC

点评:本题考查的知识要点:线面平行的判定,线面垂直的判定和性质的应用,属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=(sinα,cosα),
=(-2,1),若
⊥
,则tanα的值为( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
若复数Z1=1+i,Z2=3-i,则
=( )
| Z2 |
| Z1 |
| A、1+i | B、1+2i |
| C、1-2i | D、2-2i |
设集合A={4,5,6,8},B={3,5,7,8},则A∪B中元素的个数为( )
| A、5 | B、6 | C、7 | D、8 |
若函数f(x)=(x-1)(x-3)+(x-3)(x-4)+(x-4)(x-1),则函数f(x)的两个零点分别位于区间( )
| A、(1,3)和(3,4)内 |
| B、(-∞,1)和(1,3)内 |
| C、(3,4)和(4,+∞)内 |
| D、(-∞,1)和(4,+∞)内 |