题目内容
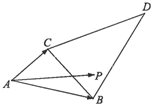
如图,△BCD与△ABC的面积之比为2,点P是区域ABCD内任意一点(含边界),且
=λ
+μ
(λ,μ∈R),则λ+μ的取值范围是( )
| AP |
| AB |
| AC |

| A、[0,1] |
| B、[0,2] |
| C、[0,3] |
| D、[0,4] |
考点:平面向量的基本定理及其意义
专题:计算题,平面向量及应用
分析:将图形特殊化,设AD垂直平分BC于O,则DO=2AO,P在A时,λ+μ=0,此时为最小;P在D时,λ+μ=3,此时为最大.
解答:
解:将图形特殊化,设AD垂直平分BC于O,则DO=2AO,
P在A时,λ=0,μ=0,所以λ+μ=0,此时为最小;
P在D时,
=3
=3×(
+
),λ=
,μ=
,所以λ+μ=3,此时为最大.
故选:C.
P在A时,λ=0,μ=0,所以λ+μ=0,此时为最小;
P在D时,
| AD |
| AO |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| 3 |
| 2 |
| 3 |
| 2 |
故选:C.
点评:本题考查平面向量基本定理,考查特殊化方法,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=x3-22-x的零点为x0,则x0所在的大致区间是( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
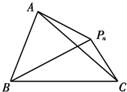 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
( )
| A、65 | B、63 | C、33 | D、31 |
若函数f(x)=(x-1)(x-3)+(x-3)(x-4)+(x-4)(x-1),则函数f(x)的两个零点分别位于区间( )
| A、(1,3)和(3,4)内 |
| B、(-∞,1)和(1,3)内 |
| C、(3,4)和(4,+∞)内 |
| D、(-∞,1)和(4,+∞)内 |
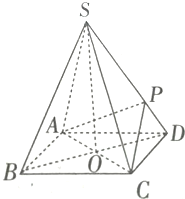 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱长都是底面边长的