题目内容
若含有三个实数的集合A可表示为{a,
,1},也可表示为{a2,a+b,0},求a1+b2+a3+a4+…+a2013+b2014的值.
| b |
| a |
考点:集合的相等
专题:集合
分析:根据题意可得{a,
,1}={a2,a+b,0},由集合相等的意义可得a=0或
=0,结合分式的性质分析可得b=0,进而可得a2=1,即a=1或a=-1,结合集合元素的性质,分析可得a的值,将a、b的值,代入计算即可.
| b |
| a |
| b |
| a |
解答:
解:∵集合A可表示为{a,
,1},也可表示为{a2,a+b,0},
∴b=0,a2=1,a+b≠1,
∴a=-1,b=0,
∴a1+b2+a3+a4+…+a2013+b2014=(-1)+(-1)+(-1)+…+(-1)=-1007
| b |
| a |
∴b=0,a2=1,a+b≠1,
∴a=-1,b=0,
∴a1+b2+a3+a4+…+a2013+b2014=(-1)+(-1)+(-1)+…+(-1)=-1007
点评:本题考查集合相等的定义与集合元素的性质,关键是由集合相等的含义,得到a、b的值,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log2x,则f(-8)值为( )
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
直线x+y=0被圆(x-2)2+y2=4截得的弦长为( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、2 |
若复数Z1=1+i,Z2=3-i,则
=( )
| Z2 |
| Z1 |
| A、1+i | B、1+2i |
| C、1-2i | D、2-2i |
 已知三棱柱ABC-A1B1C1.
已知三棱柱ABC-A1B1C1.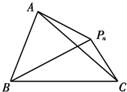 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,