题目内容
设l、m是两条不同的直线,α,β是两个不同的平面,则下列命题为真命题的是( )
| A、若m∥l,m∥α,则l∥α |
| B、若m⊥α,l⊥m,则l∥α |
| C、若α∥β,l⊥α,m∥β,则l⊥m |
| D、若m?α,m∥β,l?β,l∥α,则α∥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间直线的位置关系以及线面平行、面面平行的判定定理对选项分别分析解答.
解答:
解:对于A,若m∥l,m∥α,则l可能在α内,故A错误;
对于B,若m⊥α,l⊥m,则l可能在α内,故B错误;
对于C,若α∥β,l⊥α,得到l⊥β,结合m∥β,得到l⊥m;故C正确;
对于D,若m?α,m∥β,l?β,l∥α,则α与β可能相交;故D错误;
故选C.
对于B,若m⊥α,l⊥m,则l可能在α内,故B错误;
对于C,若α∥β,l⊥α,得到l⊥β,结合m∥β,得到l⊥m;故C正确;
对于D,若m?α,m∥β,l?β,l∥α,则α与β可能相交;故D错误;
故选C.
点评:本题考查了空间直线的位置关系以及线面平行、面面平行的判定定理,关键是熟练掌握定理.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知向量
=(3cosα,2)与向量
=(3,4sinα)平行,则锐角α等于( )
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数y=logax(a>0,a≠1)的图象经过点(2,
),则其反函数的解析式为( )
| 1 |
| 2 |
| A、y=4x | ||
| B、y=log4x | ||
| C、y=2x | ||
D、y=(
|
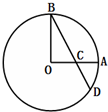 如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=
如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=