题目内容
设函数f(x)=a1•sin(x+α1)+a2•sin(x+α2)+…+αn•sin(x+αn),其中αi(i=1,2,…,n,n∈N*,n≥2)为已知实常数,x∈R,则下列命题中错误的是( )
A、若f(0)=f(
| ||
| B、若f(0)=0,则函数f(x)为奇函数 | ||
C、若f(
| ||
D、当f2(0)+f2(
|
考点:两角和与差的正弦函数,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:A.由若f(0)=f(
)=0,证明函数f(x)既是奇函数又是偶函数即可得到f(0)=0;
B.根据奇函数的定义即可得到结论;
C.根据偶函数的定义进行判断即可得到结论;
D.根据f(x1)=f(x2)=0,得(sinx1-sinx2)(a1cosα1+…+ancosαn)+(cosx1-cosx2)(a1sinα1+…+ansinαn),故可得结论.
| π |
| 2 |
B.根据奇函数的定义即可得到结论;
C.根据偶函数的定义进行判断即可得到结论;
D.根据f(x1)=f(x2)=0,得(sinx1-sinx2)(a1cosα1+…+ancosαn)+(cosx1-cosx2)(a1sinα1+…+ansinαn),故可得结论.
解答:
解答:解:A.若f(0)=0,则f(0)=a1•sin(α1)+a2•sin(α2)+…+an•sin(αn)=0,
则f(-x)+f(x)=a1•sin(-x+α1)+a2•sin(-x+α2)+…+an•sin(-x+αn)+a1•sin(x+α1)+a2•sin(x+α2)+…+an•sin(x+αn)
=cosx[a1•sinα1+a2•sinα2+…+an•sinαn]=0,∴函数f(x)为奇函数;
若f(
)=0,则f(
)=-a1•cosα1-a2•cosα2+…-an•cosαn=0,
∴f(-x)-f(x)=a1•sin(-x+α1)+a2•sin(-x+α2)+…+an•sin(-x+αn)-a1•sin(x+α1)-a2•sin(x+α2)-…-an•sin(x+αn)
=sinx[a1•cosα1+a2•cosα2+…+an•cosαn]=0,∴函数f(x)为偶函数;
则若f(0)=f(
)=0,则函数f(x)为既是奇函数又是偶函数,即f(x)=0,
∴f(x)=0对任意实数x恒成立;故A正确.
B.由A的证明过程可知当f(0)=0时,函数f(x)为奇函数,正确.
C.由A的证明过程可知当f(
)=0时,函数f(x)为偶函数,正确.
D当f2(0)+f2(
)≠0时,若f(x1)=f(x2)=0,
则f(x1)=a1•sin(x1+α1)+a2•sin(x1+α2)+…+an•sin(x1+αn)=a1•sin(x2+α1)+a2•sin(x2+α2)+…+an•sin(x2+αn)=0,
∴(sinx1-sinx2)(a1cosα1+…+ancosαn)+(cosx1-cosx2)(a1sinα1+…+ansinαn)=0,
∴sinx1-sinx2=0
可得x1-x2=kπ(k∈Z).∴D错误.
故选:D.
则f(-x)+f(x)=a1•sin(-x+α1)+a2•sin(-x+α2)+…+an•sin(-x+αn)+a1•sin(x+α1)+a2•sin(x+α2)+…+an•sin(x+αn)
=cosx[a1•sinα1+a2•sinα2+…+an•sinαn]=0,∴函数f(x)为奇函数;
若f(
| π |
| 2 |
| π |
| 2 |
∴f(-x)-f(x)=a1•sin(-x+α1)+a2•sin(-x+α2)+…+an•sin(-x+αn)-a1•sin(x+α1)-a2•sin(x+α2)-…-an•sin(x+αn)
=sinx[a1•cosα1+a2•cosα2+…+an•cosαn]=0,∴函数f(x)为偶函数;
则若f(0)=f(
| π |
| 2 |
∴f(x)=0对任意实数x恒成立;故A正确.
B.由A的证明过程可知当f(0)=0时,函数f(x)为奇函数,正确.
C.由A的证明过程可知当f(
| π |
| 2 |
D当f2(0)+f2(
| π |
| 2 |
则f(x1)=a1•sin(x1+α1)+a2•sin(x1+α2)+…+an•sin(x1+αn)=a1•sin(x2+α1)+a2•sin(x2+α2)+…+an•sin(x2+αn)=0,
∴(sinx1-sinx2)(a1cosα1+…+ancosαn)+(cosx1-cosx2)(a1sinα1+…+ansinαn)=0,
∴sinx1-sinx2=0
可得x1-x2=kπ(k∈Z).∴D错误.
故选:D.
点评:点评:本题的考点是数列与三角函数的综合,主要考查三角函数的化简,考查新定义三角函数的性质,运算量较大,有一定的难度.

练习册系列答案
相关题目
向边长分别为5,6,
的三角形区域内随机投一点M,则该点M与三角形三个顶点距离都大于1的概率为( )
| 13 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
一简单组合体的三视图如图所示,则该组合体的体积为( )


| A、16-π | B、12-4π |
| C、12-2π | D、12-π |
从[0,10]中任取一个数x,从[0,6]中任取一个数y,则使|x-5|+|y-3|≤4的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
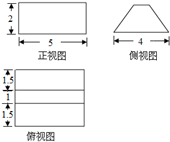
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )

A、
| ||
| B、50cm3 | ||
C、
| ||
| D、25cm3 |
若实数x,y满足
,则实数m=
的取值范围是( )
|
| y-1 |
| x+1 |
| A、(-1,1) | ||||
| B、[-1,1) | ||||
C、(-
| ||||
D、[-
|
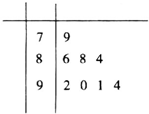 某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是
某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是