题目内容
若实数x,y满足
,则实数m=
的取值范围是( )
|
| y-1 |
| x+1 |
| A、(-1,1) | ||||
| B、[-1,1) | ||||
C、(-
| ||||
D、[-
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:作出可行域,m=
表示区域内的点与C(-1,1)连线的斜率,即可得出结论.
| y-1 |
| x+1 |
解答:
 解:作图,A(2,0),B(4,2),
解:作图,A(2,0),B(4,2),
m=
表示区域内的点与C(-1,1)连线的斜率,
∵AC的斜率为
=-
,OB的斜率为
,
∴可得实数m=
的取值范围是[-
,
).
故选:D.
 解:作图,A(2,0),B(4,2),
解:作图,A(2,0),B(4,2),m=
| y-1 |
| x+1 |
∵AC的斜率为
| 0-1 |
| 2+1 |
| 1 |
| 3 |
| 1 |
| 2 |
∴可得实数m=
| y-1 |
| x+1 |
| 1 |
| 3 |
| 1 |
| 2 |
故选:D.
点评:本题考查线性规划知识,考查数形结合的数学思想,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
设函数f(x)=a1•sin(x+α1)+a2•sin(x+α2)+…+αn•sin(x+αn),其中αi(i=1,2,…,n,n∈N*,n≥2)为已知实常数,x∈R,则下列命题中错误的是( )
A、若f(0)=f(
| ||
| B、若f(0)=0,则函数f(x)为奇函数 | ||
C、若f(
| ||
D、当f2(0)+f2(
|
cos
•cos
•cos(-
)=( )
| π |
| 9 |
| 2π |
| 9 |
| 23π |
| 9 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
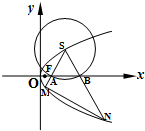 如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|= 如图,已知直线l:y=2x-4交抛物线y2=4x于A、B两点,试在抛物线AOB这段曲线上求一点P,使△ABP的面积最大,并求这个最大面积.
如图,已知直线l:y=2x-4交抛物线y2=4x于A、B两点,试在抛物线AOB这段曲线上求一点P,使△ABP的面积最大,并求这个最大面积. 已知双曲线C1:
已知双曲线C1: