题目内容
已知函数f(x)=loga(x+1),g(x)=loga(1-x)(a>0,a≠1)
(Ⅰ)求函数f(x)+g(x)的定义域并判断其奇偶性;
(Ⅱ)求使f(x)+g(x)<0成立的x的取值范围.
(Ⅰ)求函数f(x)+g(x)的定义域并判断其奇偶性;
(Ⅱ)求使f(x)+g(x)<0成立的x的取值范围.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(Ⅰ)利用对数函数的性质求函数的定义域,利用函数奇偶性的定义去判断.
(Ⅱ)需要分类讨论,当a>1和0<a<1时,根据函数的单调性得到不等式,解得即可
(Ⅱ)需要分类讨论,当a>1和0<a<1时,根据函数的单调性得到不等式,解得即可
解答:
解:(1)要使函数有意义,则有
,解得-1<x<1.
所以函数的定义域为(-1,1).
因为函数f(x)的定义域为(-1,1),关于原点对称.
所以f(-x)=loga(1-x)+loga(1+x)=f(x),
所以函数f(x)是偶函数.
(Ⅱ)∵f(x)+g(x)<0,
∴loga(1-x2)<0=loga1,
当a>1时,函数y=logax为增函数,故1-x2<1,解得x≠0,
∴x的取值范围为(-1,0)∪(0,1)
当0<a<1时,函数y=logax为减函数,故1-x2>1,解集为空集
综上所述x的取值范围为(-1,0)∪(0,1)
|
所以函数的定义域为(-1,1).
因为函数f(x)的定义域为(-1,1),关于原点对称.
所以f(-x)=loga(1-x)+loga(1+x)=f(x),
所以函数f(x)是偶函数.
(Ⅱ)∵f(x)+g(x)<0,
∴loga(1-x2)<0=loga1,
当a>1时,函数y=logax为增函数,故1-x2<1,解得x≠0,
∴x的取值范围为(-1,0)∪(0,1)
当0<a<1时,函数y=logax为减函数,故1-x2>1,解集为空集
综上所述x的取值范围为(-1,0)∪(0,1)
点评:本题主要考查了对数函数的定义和函数的奇偶性和单调性以及不等式的解法,属于基础题

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
圆(x+2)2+(y+1)2=1关于直线y=x-1对称的圆的方程为( )
| A、x2+(y-3)2=1 |
| B、x2+(y+3)2=1 |
| C、(x-3)2+y2=1 |
| D、(x+3)2+y2=1 |
已知函数f(x)=3-2|x|,g(x)=x2,构造函数F(x)=
,那么函数y=F(x)( )
|
| A、有最大值1,最小值-1 |
| B、有最小值-1,无最大值 |
| C、有最大值1,无最小值 |
| D、有最大值3,最小值1 |
函数y=
log2|x|的大致图象是( )
| x |
| |x| |
A、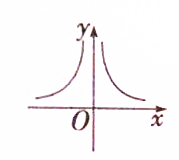 |
B、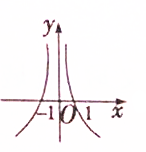 |
C、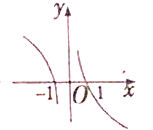 |
D、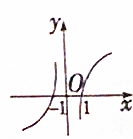 |
设i是虚数单位,若复数x满足x(1-i)=i,则其虚部为( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
 如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.
如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.