题目内容
已知一个扇形的周长为a,求当扇形的圆心角为多大时,扇形的面积最大,并求这个最大值.
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:设扇形的弧长,然后,建立关系式,结合二次函数的图象与性质求解最值即可.
解答:
解:设扇形面积为S,半径为r,圆心角为α,则扇形弧长为a-2r,
所以S=
(a-2r)r=-(r-
)2+
.
故当r=
且α=2时,扇形面积最大为
.
所以S=
| 1 |
| 2 |
| a |
| 4 |
| a2 |
| 16 |
故当r=
| a |
| 4 |
| a2 |
| 16 |
点评:本题重点考查了扇形的面积公式、弧长公式、二次函数的最值等知识,属于基础题.

练习册系列答案
相关题目
已知△ABC,∠A=120°,
•
=-2,
=
,点G是CD 上的一点,
=
+m
,则|
|的最小值为( )
| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AG |
| 1 |
| 3 |
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在斜三角形ABC中,“A>B”是“|tanA|>|tanB|”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
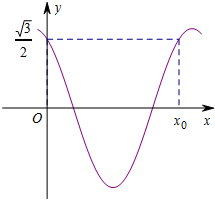 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<