题目内容
如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则| BC |
| AD |
考点：与圆有关的比例线段
专题：直线与圆,立体几何
分析：由已知条件推导出△PBC∽△PDA，由此能求出
的值．
| BC |
| AD |
解答：
（本小题12分）
解：∵ABCD四点共圆，∴∠DAB=∠PCB，
∠CDA=∠PBC，∴∠P为公共角，
∴△PBC∽△PDA，
∴
=
=
，
∴
=
=
．
解：∵ABCD四点共圆，∴∠DAB=∠PCB，
∠CDA=∠PBC，∴∠P为公共角，
∴△PBC∽△PDA，
∴
| PB |
| PD |
| PC |
| PA |
| BC |
| AD |
∴
| BC |
| AD |
| PB |
| PD |
| 1 |
| 3 |
点评：本题考查两条线段的比值的求法，是中档题，解题时要认真审题，注意四点共圆与相似三角形的性质的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
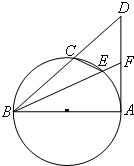如图，BA是圆O的直径，C、E在圆0上，BC、BE的延长线交直线AD于点D、F，BA2=BC•BD．求证：