题目内容
已知函数f(x)=
,g(x)=alnx,a∈R.若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值和该切线方程.
| x |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:先求出交点,再根据切线相等求出a,最后由直线上一点及斜率求出直线方程即可.
解答:
解:∵函数f(x)=
,g(x)=alnx,a∈R.
∴f′(x)=
,g′(x)=
(x>0),
由已知曲线y=f(x)与曲线y=g(x)在交点处有相同的切线,
故有
=alnx且
=
,
解得a=
,x=e2,
∵两条曲线交点的坐标为(e2,e)切线的斜率为k=f′(e2)=
,
∴切线的方程为y-e=
(x-e2).
| x |
∴f′(x)=
| 1 | ||
2
|
| a |
| x |
由已知曲线y=f(x)与曲线y=g(x)在交点处有相同的切线,
故有
| x |
| 1 | ||
2
|
| a |
| x |
解得a=
| e |
| 2 |
∵两条曲线交点的坐标为(e2,e)切线的斜率为k=f′(e2)=
| 1 |
| 2e |
∴切线的方程为y-e=
| 1 |
| 2e |
点评:本题考查利用导数研究曲线上某点切线方程,考查导数的几何意义,正确求导是关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
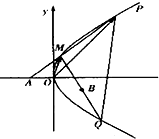 已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图
已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图 如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则
如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则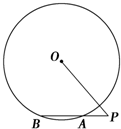 如图所示,过点P的直线与⊙O相交于A,B两点.若PA=1,AB=2,PO=3,求⊙O的半径r.
如图所示,过点P的直线与⊙O相交于A,B两点.若PA=1,AB=2,PO=3,求⊙O的半径r.