题目内容
求证：
+
+…+
＜
．
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| (2n)(2n+1) |
| 1 |
| 3 |
考点：反证法与放缩法
专题：选作题,反证法
分析：利用（2n）（2n+1）＞（2n-1）（2n+1），可得
＜
=
（
-
），即可证明结论．
| 1 |
| (2n)(2n+1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答：
证明：∵（2n）（2n+1）＞（2n-1）（2n+1），
∴
＜
=
（
-
），
∴
+
+…+
＜
+
（+
-
+…+
-
）=
+
（
-
）＜
．
即
+
+…+
＜
．
∴
| 1 |
| (2n)(2n+1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| (2n)(2n+1) |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+1 |
| 1 |
| 3 |
即
| 1 |
| 2×3 |
| 1 |
| 4×5 |
| 1 |
| (2n)(2n+1) |
| 1 |
| 3 |
点评：本题考查放缩法，考查学生分析解决问题的能力，利用
＜
=
（
-
）是关键．
| 1 |
| (2n)(2n+1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
练习册系列答案
相关题目
如图，已知一四棱锥P-ABCD的底面是边长为1的正方形，且侧棱PC⊥底面ABCD，且PC=2，E是侧棱PC上的动点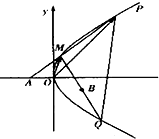
已知点A（-1，0），B（1，-1）和抛物线C：y2=4x，O为坐标原点，过点A的动直线l交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图
如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则