题目内容
已知点A（2，1），B（3，2），向量
=（-3，3）．
（1）若四边形ABCD为平行四边形，求它的两条对角线所成的锐角的余弦值；
（2）设O为坐标原点，P是直线OB上的一点，当
•
取得最小值时，求△PAD的面积．
| AD |
（1）若四边形ABCD为平行四边形，求它的两条对角线所成的锐角的余弦值；
（2）设O为坐标原点，P是直线OB上的一点，当
| PA |
| PD |
考点：平面向量数量积的运算,平面向量共线（平行）的坐标表示
专题：计算题,平面向量及应用
分析：（1）先求D点坐标，然后根据四边形ABCD为平行四边形，求出C点坐标，根据向量的夹角公求两条对角线所成的锐角的余弦值；
（2）根据P是直线OB上的一点，用λ表示出P点坐标，
•
就可表示成关于λ的二次函数，当
•
取得最小值时，求出λ的值，得出P点坐标，进而求出△PAD的面积．
（2）根据P是直线OB上的一点，用λ表示出P点坐标，
| PA |
| PD |
| PA |
| PD |
解答：
解：（1）∵点A（2，1），向量
=（-3，3）
∴D点坐标为（-1，4）
∵四边形ABCD为平行四边形，
∴
=
，
设C点的坐标为（a，b），则
=(a-3，b-2)
∴a-3=-3，b-2=3
解得：a=0，b=5
∴C点坐标为（0，5）
∴
=（-2，4），
=（-4，2）
由向量的夹角公式得：cos＜
，
＞=
=
，
∴两条对角线所成的锐角的余弦值为
．
（2）∵P是直线OB上的一点，设P点的坐标为（3λ，2λ）
•
=（2-3λ，1-2λ）•（-1-3λ，4-2λ）
=13λ2-13λ+2
当λ=
时，
•
取得最小值，
∴P点的坐标为（
，1）
∴△PAD的面积为
×
×3=
．
| AD |
∴D点坐标为（-1，4）
∵四边形ABCD为平行四边形，
∴
| AD |
| BC |
设C点的坐标为（a，b），则
| BC |
∴a-3=-3，b-2=3
解得：a=0，b=5
∴C点坐标为（0，5）
∴
| AC |
| BD |
由向量的夹角公式得：cos＜
| AC |
| BD |
| -2×(-4)+4×2 | ||||
|
| 4 |
| 5 |
∴两条对角线所成的锐角的余弦值为
| 4 |
| 5 |
（2）∵P是直线OB上的一点，设P点的坐标为（3λ，2λ）
| PA |
| PD |
=13λ2-13λ+2
当λ=
| 1 |
| 2 |
| PA |
| PD |
∴P点的坐标为（
| 3 |
| 2 |
∴△PAD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
点评：本题考查了向量的运算及函数的最值问题，研究最值时关键是通过构造函数来解决．
练习册系列答案
相关题目
在△ABC中，已知
如图，已知BC为⊙O的直径，点A、F在⊙O上，AD⊥BC，垂足为D，BF交AD于E，且AE=BE．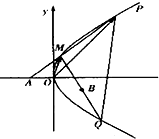
已知点A（-1，0），B（1，-1）和抛物线C：y2=4x，O为坐标原点，过点A的动直线l交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图
如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则