题目内容
已知双曲线两个焦点分别为F1（-10，0），F2（10，0），双曲线上一点P到F1，F2距离差的绝对值等于12，求双曲线的标准方程．
考点：双曲线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：利用双曲线的第一定义直接求解．
解答：
解：∵双曲线两个交点分别为F1（-10，0），F2（10，0），
双曲线上一点P到F1，F2距离差的绝对值等于12，
∴设所求的双曲线方程为
-
=1，
且
，∴b2=100-36=64，
∴所求双曲线的标准方程为
-
=1．
双曲线上一点P到F1，F2距离差的绝对值等于12，
∴设所求的双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
且
|
∴所求双曲线的标准方程为
| x2 |
| 100 |
| y2 |
| 64 |
点评：本题考查双曲线方程的求法，是基础题，解题时要认真审题，注意双曲线的定义的合理运用．
练习册系列答案
相关题目
从只有3张中奖的10张彩票中不放回随机逐张抽取，设X表示直至抽到中奖彩票时的次数，则P（X=3）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
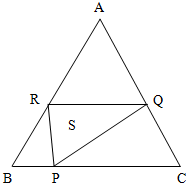如图，在正△ABC的边BC、CA、AB上分别取点P、Q、R，使CQ=2BP，AR=3BP．已知正三角形的边长是11cm，BP=xcm，△PQR的面积为S