题目内容
从只有3张中奖的10张彩票中不放回随机逐张抽取,设X表示直至抽到中奖彩票时的次数,则P(X=3)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率
专题:计算题,概率与统计
分析:确定从只有3张中奖的10张彩票中不放回随机逐张抽取,所有的情况;前两次没有中奖,最后一次中奖的情况,利用古典概型概率公式,即可求解.
解答:
解:因为从只有3张中奖的10张彩票中不放回随机逐张抽取,那么所有的情况为
,而X表示直至抽到中奖彩 票时的次数为3,那么前两次没有中奖,最后一次中奖的情况为
,
因此概率值为
,
故选:D.
| A | 3 10 |
| C | 1 7 |
| C | 1 6 |
| C | 1 3 |
因此概率值为
| 7 |
| 40 |
故选:D.
点评:等可能事件的概率计算,关键是确定基本事件的情况总数.

练习册系列答案
相关题目
若关于x的不等式ax2-2ax+1≤0无解,则实数a的取值集合为( )
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |
计算
dx的结果是( )
| ∫ | e 1 |
| 1 |
| x |
| A、e |
| B、1-e-2 |
| C、1 |
| D、e-1 |
某产品的广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程
=
x+
中的
为9.4,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 3.5 | 3.8 | 4 | 4.7 |
| 销售费用x(万元) | 27 | 37 | 47 | 49 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、63.6万元 |
| B、58.8万元 |
| C、67.7万元 |
| D、72.0万元 |
已知角α的终边经过点(3a,-4a)(a<0),则sinα+cosα等于( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
函数y=x2+1在x=2处的导数是( )
| A、5 | B、4 | C、3 | D、2 |
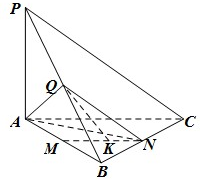 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.