题目内容
已知tanθ=2,求f(x)=
的值.
sin(θ-
| ||||
cos(π+θ)+2cos(
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:根据tanθ=2,把要求的式子利用同角三角函数的基本关系化为
,即
,计算求得结果
| 2sinθ-3cosθ |
| -2sinθ-5cosθ |
| 2tanθ-3 |
| -2tanθ-5 |
解答:
解:∵已知tanθ=2,
∴f(x)=
=
=
=
=
=-
.
∴f(x)=
sin(θ-
| ||||
cos(π+θ)+2cos(
|
-sin(
| ||||
| -cosθ-2sinθ+4cos(π-θ) |
| cosθ+2sinθ-4cosθ |
| -cosθ-2sinθ-4cosθ |
| 2sinθ-3cosθ |
| -2sinθ-5cosθ |
| 2tanθ-3 |
| -2tanθ-5 |
| 1 |
| 9 |
点评:本题主要考查同角三角函数的基本关系的应用,诱导公式的应用,注意三角函数在各个象限中的符号,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
某产品的广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程
=
x+
中的
为9.4,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 3.5 | 3.8 | 4 | 4.7 |
| 销售费用x(万元) | 27 | 37 | 47 | 49 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、63.6万元 |
| B、58.8万元 |
| C、67.7万元 |
| D、72.0万元 |
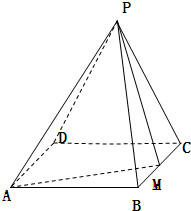 如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=