题目内容
在全国汉字听写大赛之前,某地先进行了共十轮的选拔赛,某研究机构一直关注其测试选拔过程.第二轮选拔后有450名学生进入下一轮,该机构利用分层抽样的方法抽取了90人进行跟踪调查,得到第三轮是否通过的数据如下表所示:
(Ⅰ)利用独立性检验估计第三轮通过与否与学生的性别是否有关?
(Ⅱ)估计全部450名学生通过第三轮测试的大约有多少人?
(Ⅲ)如果从第三轮测试通过的所有学生中利用分层抽样的方法抽取6名学生,然后从这6名学生中随机抽取2名学生进行问卷调查,求着2名学生中至少有1名女学生的概率.
附:K2=
(其中n=a+b+c+d)
| 考试未通过 | 考试通过 | 总计 | |
| 女学生 | 27 | 36 | 63 |
| 男学生 | 9 | 18 | 27 |
| 总计 | 36 | 54 | 90 |
(Ⅱ)估计全部450名学生通过第三轮测试的大约有多少人?
(Ⅲ)如果从第三轮测试通过的所有学生中利用分层抽样的方法抽取6名学生,然后从这6名学生中随机抽取2名学生进行问卷调查,求着2名学生中至少有1名女学生的概率.
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
考点:独立性检验的应用,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(Ⅰ)计算K2,与临界值比较,即可得出结论;
(Ⅱ)求出学生通过第三轮测试的频率,即可估计全部450名学生通过第三轮测试的大约有多少人?
(Ⅲ)利用列举法确定从这6名学生中随机抽取2名学生的情况,至少有1名女生的取法,即可求出概率.
(Ⅱ)求出学生通过第三轮测试的频率,即可估计全部450名学生通过第三轮测试的大约有多少人?
(Ⅲ)利用列举法确定从这6名学生中随机抽取2名学生的情况,至少有1名女生的取法,即可求出概率.
解答:
解:(Ⅰ)根据公式得,K2=
=
=0.71<1.323
…(2分)
所以我们认为是否通过第三轮测试与学生的性别无关.…(3分)
(Ⅱ)由样本数据可知,学生通过第三轮测试的频率为
=0.6.…(4分)
故450名学生中通过第三轮测试的大约有450×0.6=270(人) …(6分)
(Ⅲ)根据表格,通过第三轮测试的男同学有36人,女同学18人,…(7分)
由分层抽样可知,抽取的6名学生中男学生有4名,分别记为A,B,C,D,女学生为2名,分别记为1,2.从中任选2名的不同取法为{A,B},{A,C},{A,D},{A,1},{A,2},{B,C},{B,D},{B,1},{B,2},{C,D},{C,1},{C,2},{D,1},{D,2},{1,2},共15种.…(10分)
其中至少有1名女生的取法为{A,1},{A,2},{B,1},{B,2},{C,1},{C,2},{D,1},{D,2},
{1,2},共9种.…(11分)
所以所求事件的概率为
=
.…(12分)
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 90×(27×18-36×9)2 |
| 63×27×36×54 |
…(2分)
所以我们认为是否通过第三轮测试与学生的性别无关.…(3分)
(Ⅱ)由样本数据可知,学生通过第三轮测试的频率为
| 54 |
| 90 |
故450名学生中通过第三轮测试的大约有450×0.6=270(人) …(6分)
(Ⅲ)根据表格,通过第三轮测试的男同学有36人,女同学18人,…(7分)
由分层抽样可知,抽取的6名学生中男学生有4名,分别记为A,B,C,D,女学生为2名,分别记为1,2.从中任选2名的不同取法为{A,B},{A,C},{A,D},{A,1},{A,2},{B,C},{B,D},{B,1},{B,2},{C,D},{C,1},{C,2},{D,1},{D,2},{1,2},共15种.…(10分)
其中至少有1名女生的取法为{A,1},{A,2},{B,1},{B,2},{C,1},{C,2},{D,1},{D,2},
{1,2},共9种.…(11分)
所以所求事件的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题主要考查了独立性检验知识,考查概率的计算,同时考查了分析问题的能力和运算求解的能力,属于中档题

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
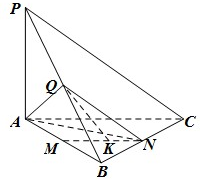 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.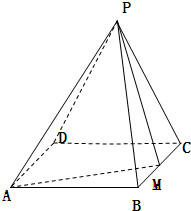 如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=