题目内容
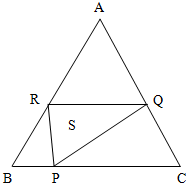 如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S
如图,在正△ABC的边BC、CA、AB上分别取点P、Q、R,使CQ=2BP,AR=3BP.已知正三角形的边长是11cm,BP=xcm,△PQR的面积为S(1)用解析式将S表示成x的函数;
(2)求S的最小值及相应的x值.
考点:函数解析式的求解及常用方法,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)首先,求解△ABC、△BPR、△PCQ、△ARQ的面积,然后,求解得到将S表示成x的函数;
(2)根据(1),借助于二次函数的性质求解最值即可.
(2)根据(1),借助于二次函数的性质求解最值即可.
解答:
解:(1)∵BP=xcm,
∴AR=3x,CQ=2x,
∴BR=11-3x,
△BPR中,BP边上的高为
,
△PCQ中,PC边上的高为
,
△ARQ中,AR边上的高为
,
∴S=S△ABC-(S△BPR+S△PCQ+S△ARQ)
=
(x2-6x+11),
∴S=
(x2-6x+11),(0<x<11),
(2)根据(1),
S=
(x2-6x+11),
=
[(x-3)2+2],
∵0<x<11,
∴当x=3时,S有最小值
.
∴AR=3x,CQ=2x,
∴BR=11-3x,
△BPR中,BP边上的高为
| ||
| 2 |
△PCQ中,PC边上的高为
2
| ||
| 2 |
△ARQ中,AR边上的高为
| ||
| 2 |
∴S=S△ABC-(S△BPR+S△PCQ+S△ARQ)
=
11
| ||
| 4 |
∴S=
11
| ||
| 4 |
(2)根据(1),
S=
11
| ||
| 4 |
=
11
| ||
| 4 |
∵0<x<11,
∴当x=3时,S有最小值
11
| ||
| 2 |
点评:本题重点考查函数的解析式的求解方法,理解自变量的取值情形是解题的关键,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算
dx的结果是( )
| ∫ | e 1 |
| 1 |
| x |
| A、e |
| B、1-e-2 |
| C、1 |
| D、e-1 |
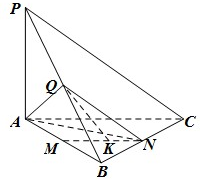 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点.