题目内容
已知函数f(x)=cos2(x-
)-sin2(x-
)-
sin(x-
)cosx.
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)锐角三角形ABC的三内角分别为角A、B、C且f(
-
)=
,求sinB+sinC的取值范围.
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)锐角三角形ABC的三内角分别为角A、B、C且f(
| A |
| 2 |
| π |
| 8 |
2+
| ||
| 4 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的图像与性质
分析:(Ⅰ)对函数解析式化简,进而利用正弦函数的性质求得函数f(x)的单调增区间.
(Ⅱ)利用f(
-
)的值求得∠A,进而求得∠B的范围,对sinB+sinC进行变形化简,进而根据∠B的范围求得其取值范围.
(Ⅱ)利用f(
| A |
| 2 |
| π |
| 8 |
解答:
解:(Ⅰ)∵f(x)=cos2(x-
)-sin2(x-
)-
sin(x-
)cosx
=cos2(x-
)-
(
sinx-
cosx)cosx
=sin2x-sinxcosx+cos2x
=
sin2x+
cos2x+
=
sin(2x+
)+
∴当2kπ-
≤2x+
≤2k+
(k∈Z)时,即kπ-
≤x≤kπ+
(k∈Z),函数f(x)单调增,
∴函数f(x)的单调增区间为[kπ-
,kπ+
](k∈Z).
(2)∵f(
-
)=
sin(A+
)+
=
,
∴sinA=
∵三角形ABC为锐角三角形,
∴∠A=
∵0<∠C<
,∠C=
-∠B
∴
<∠B<
,
∴sinB+sinC=sinB+sin(B+
)=
sinB+
cosB=
sin(B+
)
∵
<∠B<
,
∴
<B+
<
,
∴
<sin(B+
)≤1
∴
<
sin(B+
)≤
∴sinB+sinC的取值范围是(
,
].
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
=cos2(x-
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin2x-sinxcosx+cos2x
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴当2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(2)∵f(
| A |
| 2 |
| π |
| 8 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
2+
| ||
| 4 |
∴sinA=
| ||
| 2 |
∵三角形ABC为锐角三角形,
∴∠A=
| π |
| 3 |
∵0<∠C<
| π |
| 2 |
| 2π |
| 3 |
∴
| π |
| 6 |
| π |
| 2 |
∴sinB+sinC=sinB+sin(B+
| π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵
| π |
| 6 |
| π |
| 2 |
∴
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴
| ||
| 2 |
| π |
| 6 |
∴
| 3 |
| 2 |
| 3 |
| π |
| 6 |
| 3 |
∴sinB+sinC的取值范围是(
| 3 |
| 2 |
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数的基本性质.做此类题要求学生对三角函数基本性质,相关公式熟练记忆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=x2+1在x=2处的导数是( )
| A、5 | B、4 | C、3 | D、2 |
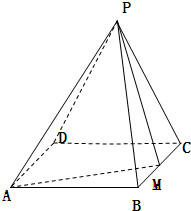 如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,△PCD为等边三角形,BC=