题目内容
已知函数f(x)=ax-3,g(x)=bx-1+cx-2(a,b∈R)且g(-
)-g(1)=f(0).
(1)试求b,c所满足的关系式;
(2)若b=0,集合A={x|f(x)≥x|x-a|g(x)},试求集合A.
| 1 |
| 2 |
(1)试求b,c所满足的关系式;
(2)若b=0,集合A={x|f(x)≥x|x-a|g(x)},试求集合A.
考点:利用导数研究函数的单调性
专题:分类讨论
分析:(1)由g(-
)-g(1)=f(0)得出b,c的关系;
(2)运用分类讨论思想,对实数a进行讨论,较两方程根的大小,结合二次函数图象,求出集合A.
| 1 |
| 2 |
(2)运用分类讨论思想,对实数a进行讨论,较两方程根的大小,结合二次函数图象,求出集合A.
解答:
解:(1)由g(-
)-g(1)=f(0),得-2b+4c-(b+c)=-3,即b,c所满足的关系式b-c-1=0;
(2)当b=0时,c=-1,∴g(x)=-
,f(x)≥x|x-a|g(x)
?ax-3≥
?
,
①当a=0时原不等式等价于-3≥
此时A=∅,
②当a>0时,根据x-a=3x-ax2解得x1,2=
(要根据a的正负区别两根大小,即左右)
a-x=3x-ax2解得x3,4=
,
∴当a∈(0,
]时,A=(0,
]∪[
,+∞),
当a∈(
,2)时,A=(0,
]∪[
,+∞),
当a∈[2,+∞)时,A=(0,+∞)
③当a<0时
当a∈[-
,0)时,A=(0,
]∪(-∞,
],
当a∈(-∞,-
),A=(0,
]∪(-∞,
].
| 1 |
| 2 |
(2)当b=0时,c=-1,∴g(x)=-
| 1 |
| x2 |
?ax-3≥
| -|x-a| |
| x |
|
①当a=0时原不等式等价于-3≥
| -|x| |
| x |
②当a>0时,根据x-a=3x-ax2解得x1,2=
1±
| ||
| a |
a-x=3x-ax2解得x3,4=
2±
| ||
| a |
∴当a∈(0,
| 3 |
1-
| ||
| a |
1+
| ||
| a |
当a∈(
| 3 |
2-
| ||
| a |
2+
| ||
| a |
当a∈[2,+∞)时,A=(0,+∞)
③当a<0时
当a∈[-
| 3 |
1-
| ||
| a |
1+
| ||
| a |
当a∈(-∞,-
| 3 |
1-
| ||
| a |
1+
| ||
| a |
点评:本题考查了,等价转换思想,分类讨论思想,二次函数.属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
向量
=(3,4)在向量
=(7,-24)上的投影是( )
| a |
| b |
| A、3 | B、-3 | C、15 | D、-15 |
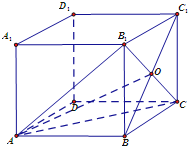 如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.
如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.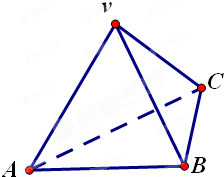 如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2