题目内容
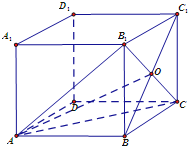 如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.
如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.(1)求直线AO与直线C1D1所成角的余弦值;
(2)求直线AO与平面BCC1B1所成角的正弦值;
(2)求二面角D-AC-B1的正切值.
考点:用空间向量求平面间的夹角,异面直线及其所成的角,直线与平面所成的角
专题:空间角
分析:(1)设正方体ABCD-A1B1C1D1的棱长为2,以D为原点,建立空间直角坐标系,利用向量法能求出直线AO与直线C1D1所成角的余弦值.
(2)求出平面BCC1B1的法向量和
,利用向量法能求出直线AO与平面BCC1B1所成角的正弦值.
(3)求出平面ACB1的法向量和平面ACD的法向量,利用向量法能求出二面角D-AC-B1的正切值.
(2)求出平面BCC1B1的法向量和
| AO |
(3)求出平面ACB1的法向量和平面ACD的法向量,利用向量法能求出二面角D-AC-B1的正切值.
解答:
解:(1)设正方体ABCD-A1B1C1D1的棱长为2,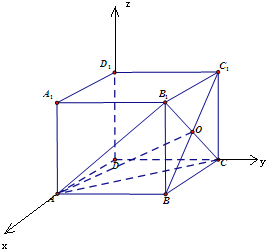
以D为原点,建立空间直角坐标系,
则A(2,0,0),O(1,2,1),
C1(0,2,2),D1(0,0,2),
=(-1,2,1),
=(0,-2,0),
|cos<
,
>|=|
|=
.
∴直线AO与直线C1D1所成角的余弦值为
.(4分)
(2)∵平面BCC1B1的法向量
=(0,1,0),
=(-1,2,1),
设直线AO与平面BCC1B1所成角为θ,
sinθ=|cos<
,
>|=|
|=
.
∴直线AO与平面BCC1B1所成角的正弦值
.(8分)
(3)A(2,0,0),C(0,2,0),B1(2,2,2),
=(-2,2,0),
=(0,2,2),
设平面ACB1的法向量
=(x,y,z),
则
,
取x=1,得
=(1,1,-1),
又平面ACD的法向量
=(0,0,1),
设二面角D-AC-B1的平面角为α,α为钝角,
∴cosα=-|cos<
,
>|=-|
|=-
,
∴tanα=-
,
∴二面角D-AC-B1的正切值为-
.(14分)

以D为原点,建立空间直角坐标系,
则A(2,0,0),O(1,2,1),
C1(0,2,2),D1(0,0,2),
| AO |
| C1D1 |
|cos<
| AO |
| C1D1 |
| -4 | ||
|
| ||
| 3 |
∴直线AO与直线C1D1所成角的余弦值为
| ||
| 3 |
(2)∵平面BCC1B1的法向量
| n |
| AO |
设直线AO与平面BCC1B1所成角为θ,
sinθ=|cos<
| AO |
| n |
| 2 | ||
|
| ||
| 3 |
∴直线AO与平面BCC1B1所成角的正弦值
| ||
| 3 |
(3)A(2,0,0),C(0,2,0),B1(2,2,2),
| AC |
| AB1 |
设平面ACB1的法向量
| m |
则
|
取x=1,得
| m |
又平面ACD的法向量
| p |
设二面角D-AC-B1的平面角为α,α为钝角,
∴cosα=-|cos<
| m |
| p |
| -1 | ||
|
| ||
| 3 |
∴tanα=-
| 2 |
∴二面角D-AC-B1的正切值为-
| 2 |
点评:本题考查直线与直线所成角的余弦值的求法,考查直线与平面所成角的正弦值的求法,考查二面角的正切值的求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
函数y=-
在x=
处的切线方程是( )
| 1 |
| x |
| 1 |
| 2 |
| A、y=4x |
| B、y=4x-4 |
| C、y=4(x+1) |
| D、y=2x-4 |
在△ABC中若A=60°,B=45°,b=2
,则a为( )
| 2 |
A、2
| ||||
B、2
| ||||
C、
| ||||
| D、2 |
用1,2,3,4这四个数字可排成必须含有重复数字的四位数有( )
| A、265个 | B、232个 |
| C、128个 | D、24个 |