题目内容
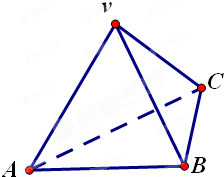 如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
如图,在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2| 3 |
(1)求二面角V-AB-C的平面角的度数;
(2)求三棱锥V-ABC的体积.
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)取AB的中点G,连接VG、CG,∠VGC是二面角V-AB-C的平面角,由此能求出二面角V-AB-C的平面角的度数.
(2)由VG⊥AB,CG⊥AB,AB⊥平面VGC,能求出三棱锥V--ABC的体积.
(2)由VG⊥AB,CG⊥AB,AB⊥平面VGC,能求出三棱锥V--ABC的体积.
解答:
解:(1)取AB的中点G,连接VG、CG
∵又VA=VB=AC=BC=2,
∴VG⊥AB,CG⊥AB
∴∠VGC是二面角V-AB-C的平面角,
在三角形VAB和三角形CAB中,
∵VA=VB=AC=BC=2,AB=2
解得VG=CG=1,
∴三角形VGC是等边三角形,∠VGC=60°.
∴二面角V-AB-C的平面角的度数为60°.
(2)∵VG⊥AB,CG⊥AB,AB⊥平面VGC,
VA=VB=AC=BC=2,AB=2
,VC=1,
∴三棱锥V--ABC的体积为:
vv-ABC=
S△VGC•|AB|=
•
•2
=
.
∵又VA=VB=AC=BC=2,
∴VG⊥AB,CG⊥AB
∴∠VGC是二面角V-AB-C的平面角,

在三角形VAB和三角形CAB中,
∵VA=VB=AC=BC=2,AB=2
| 3 |
解得VG=CG=1,
∴三角形VGC是等边三角形,∠VGC=60°.
∴二面角V-AB-C的平面角的度数为60°.
(2)∵VG⊥AB,CG⊥AB,AB⊥平面VGC,
VA=VB=AC=BC=2,AB=2
| 3 |
∴三棱锥V--ABC的体积为:
vv-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 1 |
| 2 |
点评:本题考查二面角的求法,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
等差数列{an}中,S10=120,那么a5+a6的值是( )
| A、12 | B、24 | C、36 | D、48 |
 如图,四边形ABCD中,AB=2,C=2
如图,四边形ABCD中,AB=2,C=2