题目内容

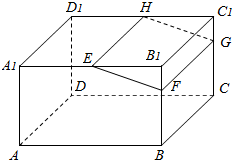如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1、CC1相交，交点分别为F、G．求证：FG∥平面ADD1A1．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：首先，证明EH∥平面B1BCC1，然后，证明EH∥FG，从而得到FG∥平面ADD1A1．
解答： 证明：∵EH∥A1D1，且B1C1∥A1D1，
∴EH∥平面B1BCC1，
∵平面EFGH∩平面B1BCC1=FG
∴EH∥FG，
∵EH∥A1D1，且EH?平面ADD1A1．
∴FG∥平面ADD1A1．
点评：本题重点考查了空间中直线与直线平行、直线与平面平行、平面和平面平行的判定和性质等知识，属于中档题，解题关键是熟练运用判定和性质定理进行解题．
练习册系列答案
相关题目
若等比数列{an}的各项均为正数，且a10a11+a9a12=2e2，则lna1+lna2+…+lna20=
 
．
已知直线l过圆（x+4）2+y2=16的圆心C且垂直与x轴，点F的坐标是（-6，0），点G是圆上任意一点．
（1）若直线FG与直线l相交 于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；
（2）过点F人作两条互相垂直的弦，设其弦长为m．n，求m+n的最大值；
（3）在平面上是否存在定点P，使得对圆C上任意的点G，都有|GP|=2|GF|？若存在，求出点P的坐标；若存在，请说明理由．
已知f（x）为奇函数，当x≥0时，f（x）=
sinπx，x∈[0，
1
2
]
log
1
2
x，x∈(
1
2
，+∞)
，则不等式f（x）≤
1
2
解集为（　　）
A、[-
2
，
1
6
]∪[
2
2
，+∞）
B、[-
2
，
1
3
]∪[
2
2
，+∞）
C、[-
2
，-
1
6
]∪[
1
6
，
2
]
D、[-
2
，
1
6
]∪[
2
，+∞）
在△ABC中，已知D是AB边上一点，若
AD
=2
DB
，
CD
=λ
CA
+μ
CB
，则λ-μ=
 
．
已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=2
6
，则球O的表面积为
 
．
函数y=2x3-3x2-12x+5在[0，3]上的最小值是
 
．
已知△ABC三边a，b，c满足a2-c2=2b，且sinAcosC=3cosAsinC，则b的值为（　　）
A、4
B、2
3
C、3
D、3
2
已知
a
=(4，2)是直线l的方向向量，直线l的倾斜角为α，则
2
cos2α+sin2α+1
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网