题目内容
已知
=(4,2)是直线l的方向向量,直线l的倾斜角为α,则
= .
| a |
| 2 |
| cos2α+sin2α+1 |
考点:二倍角的正弦,直线的倾斜角,直线的方向向量
专题:三角函数的求值,直线与圆
分析:由直线的方向向量求出直线的斜率,得到倾斜角的正切值,然后利用万能公式求得sin2α,cos2α的值,则答案可求.
解答:
解:∵知
=(4,2)是直线l的方向向量,
∴直线l的斜率为
,即tanα=
,
则sin2α=
=
=
,
cos2α=
=
=
.
∴
=
=
.
故答案为:
.
| a |
∴直线l的斜率为
| 1 |
| 2 |
| 1 |
| 2 |
则sin2α=
| 2tanα |
| 1+tan2α |
2×
| ||
1+(
|
| 4 |
| 5 |
cos2α=
| 1-tan2α |
| 1+tan2α |
1-(
| ||
1+(
|
| 3 |
| 5 |
∴
| 2 |
| cos2α+sin2α+1 |
| 2 | ||||
|
| 5 |
| 6 |
故答案为:
| 5 |
| 6 |
点评:本题考查了直线的方向向量,考查了万能公式的应用,是中档题.

练习册系列答案
相关题目
已知0≤x≤π,且-
<a<0,那么函数f(x)=cos2x-2asinx-1的最小值是( )
| 1 |
| 2 |
| A、2a+1 | B、2a-1 |
| C、-2a-1 | D、2a |
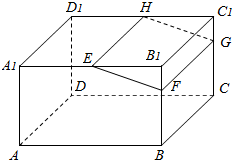 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1. 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<
函数f(x)=2sin(ωx+φ)(ω>0,0<φ< 国庆期间,某市准备将人民广场用不同的花卉装扮一个有五个区域的大型花坛(如图所示),要求相邻区域不得使用同种花卉(C与E、B与D不相邻).现有4种花卉可供选用,则不同的装扮方案共有( )
国庆期间,某市准备将人民广场用不同的花卉装扮一个有五个区域的大型花坛(如图所示),要求相邻区域不得使用同种花卉(C与E、B与D不相邻).现有4种花卉可供选用,则不同的装扮方案共有( )