题目内容
已知△ABC三边a，b，c满足a2-c2=2b，且sinAcosC=3cosAsinC，则b的值为（ ）
| A、4 | ||
B、2
| ||
| C、3 | ||
D、3
|
考点：余弦定理的应用
专题：解三角形
分析：通过正弦定理以及余弦定理化简已知表达式，然后求出的b值；
解答：
由正弦定理以及余弦定理可得：
sinAcosC=3cosAsinC
⇒a•
=3
•c
⇒2a2=b2+2c2，
又∵a2-c2=2b，
∴b=4．
故选：A．
sinAcosC=3cosAsinC
⇒a•
| a2+b2-c2 |
| 2ab |
| b2+c2-a2 |
| 2bc |
⇒2a2=b2+2c2，
又∵a2-c2=2b，
∴b=4．
故选：A．
点评：本题考查正弦定理以及余弦定理的应用，三角形的面积的求法，考查计算能力，属于中档题．
练习册系列答案
相关题目
如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于A，B两点，交其准线于点C，若|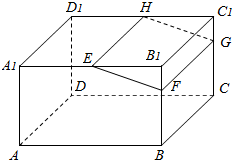
如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1、CC1相交，交点分别为F、G．求证：FG∥平面ADD1A1．
如图，平面内有三个向量
已知点P（x，y）的可行域是如图阴影部分（含边界），若目标函数z=2x-ay取得最小值的最优解有无数个，则a的值为（ ）| A、-2 | B、0 |
| C、6 | D、． 8 |
函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜