题目内容
函数y=2x3-3x2-12x+5在[0，3]上的最小值是 ．
考点：利用导数求闭区间上函数的最值
专题：计算题,导数的综合应用
分析：先求导y′=6x2-6x-12=6（x-2）（x+1），从而判断函数的单调性，再求最小值即可．
解答：
解：y′=6x2-6x-12=6（x-2）（x+1），
则y=2x3-3x2-12x++5在[0，2]上单调递减，在[2，3]上单调递增，
∴ymin=2×8-3×4-12×2+5=-15．
故答案为：-15．
则y=2x3-3x2-12x++5在[0，2]上单调递减，在[2，3]上单调递增，
∴ymin=2×8-3×4-12×2+5=-15．
故答案为：-15．
点评：本题考查了导数的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
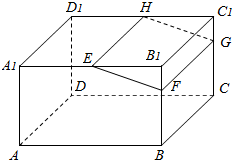如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1、CC1相交，交点分别为F、G．求证：FG∥平面ADD1A1．
如图，平面内有三个向量
函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜