题目内容

若等比数列{an}的各项均为正数，且a10a11+a9a12=2e2，则lna1+lna2+…+lna20=
 
．
考点：数列的求和
专题：等差数列与等比数列
分析：由等比数列的性质得，a10a11=a9a12=e2，根据对数的运算律化简式子，根据等比数列的性质求值．
解答： 解：因为a10a11+a9a12=2e2，
由等比数列的性质得，a10a11=a9a12=e2，
所以lna1+lna2+…+lna20
=ln（a1a2+…+a20）=ln(a10a11)10
=10lne2=20，
故答案为：20．
点评：本题考查等比数列的性质，对数的运算律的应用，难度不大．
练习册系列答案
相关题目
一个圆锥的高是10cm，侧面展开图是半圆．
（1）圆锥的侧面积是多少？
（2）轴截面等腰三角形的顶角为多少度？
已知y=f（x）是定义在（-1，1）上的奇函数，在区间[0，1）上是减函数，且f（1-a）+f（1-a2）＜0，求实数a的取值范围．
已知函数f（x）是定义在R上的奇函数，且满足f（x+2）=f（x）．若当x∈（-1，0）时，f（x）=2-x，则f(log24
2
)的值为（　　）
A、0
B、1
C、
2
D、-
2
下列五种说法：
①三个不同平面将空间最多分成8个区域；
②已知随机变量X服从正态分布N（3，1），且P（2≤X≤4）=0.6，则P（X＞4）=0.3；
③将三进制数字2011化为十进制所得的数为58；
④在一个2×2列联表中，计算得到K2的观测值k=13.079，则其中两个变量间有关系的可能性为95%；
⑤椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）中，若半焦距c＞b，记F1，F2为焦点，则椭圆上仅存在四个点P，使得∠F1PF2=90°．
你认为说法错误的是：
 
．
求下列函数的定义域：
（1）f（x）=
2x+1
x-1

（2）f（x）=
2x2+3x
．
若空间两条直线a，b没有公共点，则其位置关系是
 
．
如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于A，B两点，交其准线于点C，若|
AF
|=3，且
CB
=2
BF
，则此抛物线的方程为
 
．
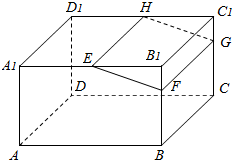如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1、CC1相交，交点分别为F、G．求证：FG∥平面ADD1A1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网