题目内容
已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=2
,则球O的表面积为 .
| 6 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:由于直三棱柱ABC-A1B1C1的底面ABC为直角三角形,我们可以把直三棱柱ABC-A1B1C1补成四棱柱,则四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积.
解答:
解:由题意,三棱柱ABC-A1B1C1为直三棱柱ABC-A1B1C1,底面ABC为直角三角形,把直三棱柱ABC-A1B1C1补成四棱柱,
则四棱柱的体对角线是其外接球的直径,
所以外接球半径为
=
,
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=4×
π=49π.
故答案为:49π.
则四棱柱的体对角线是其外接球的直径,
所以外接球半径为
| 1 |
| 2 |
32+42+(2
|
| 7 |
| 2 |
则三棱柱ABC-A1B1C1外接球的表面积是4πR2=4×
| 49 |
| 4 |
故答案为:49π.
点评:本题考查球的体积和表面积,球的内接体问题,关键是由组合体的位置关系得到球的半径,考查学生空间想象能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=1+x-
+
-
+…+
(x>0),则f(x)在定义域上的单调性是( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
| A、在(0,+∞)单调递增 |
| B、在(0,+∞)单调递减 |
| C、在(0,1)单调递增,在(1,+∞)单调递减 |
| D、在(0,1)单调递减,(1,+∞)单调递增 |
 已知点P(x,y)的可行域是如图阴影部分(含边界),若目标函数z=2x-ay取得最小值的最优解有无数个,则a的值为( )
已知点P(x,y)的可行域是如图阴影部分(含边界),若目标函数z=2x-ay取得最小值的最优解有无数个,则a的值为( )| A、-2 | B、0 |
| C、6 | D、. 8 |
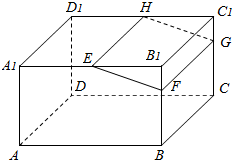 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1. 如图,平面内有三个向量
如图,平面内有三个向量 国庆期间,某市准备将人民广场用不同的花卉装扮一个有五个区域的大型花坛(如图所示),要求相邻区域不得使用同种花卉(C与E、B与D不相邻).现有4种花卉可供选用,则不同的装扮方案共有( )
国庆期间,某市准备将人民广场用不同的花卉装扮一个有五个区域的大型花坛(如图所示),要求相邻区域不得使用同种花卉(C与E、B与D不相邻).现有4种花卉可供选用,则不同的装扮方案共有( )